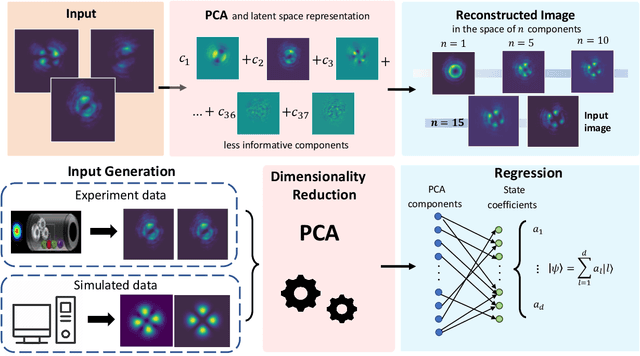
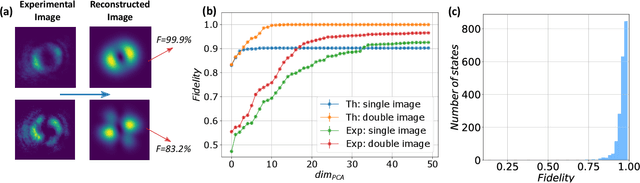
Regression of high dimensional angular momentum states of light

The Orbital Angular Momentum (OAM) of light is an infinite-dimensional degree of freedom of light with several applications in both classical and quantum optics. However, to fully take advantage of the potential of OAM states, reliable detection platforms to characterize generated states in experimental conditions are needed. Here, we present an approach to reconstruct input OAM states from measurements of the spatial intensity distributions they produce. To obviate issues arising from intrinsic symmetry of Laguerre-Gauss modes, we employ a pair of intensity profiles per state projecting it only on two distinct bases, showing how this allows to uniquely recover input states from the collected data. Our approach is based on a combined application of dimensionality reduction via principal component analysis, and linear regression, and thus has a low computational cost during both training and testing stages. We showcase our approach in a real photonic setup, generating up-to-four-dimensional OAM states through a quantum walk dynamics. The high performances and versatility of the demonstrated approach make it an ideal tool to characterize high dimensional states in quantum information protocols.

Mixed State Entanglement Classification using Artificial Neural Networks

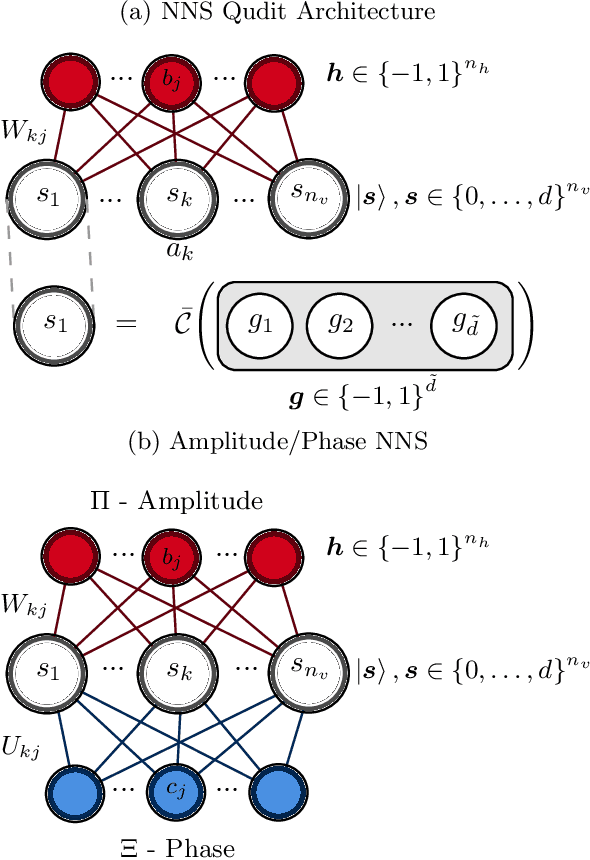
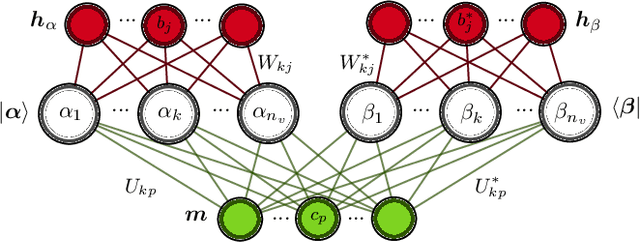
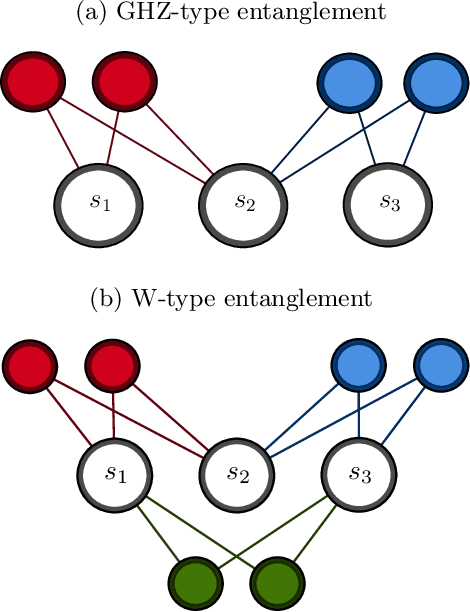
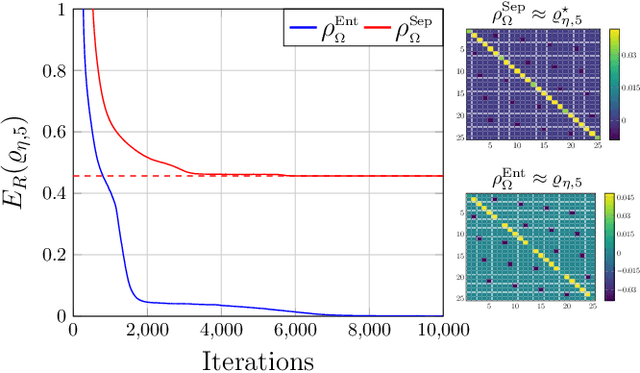
Reliable methods for the classification and quantification of quantum entanglement are fundamental to understanding its exploitation in quantum technologies. One such method, known as Separable Neural Network Quantum States (SNNS), employs a neural network inspired parameterisation of quantum states whose entanglement properties are explicitly programmable. Combined with generative machine learning methods, this ansatz allows for the study of very specific forms of entanglement which can be used to infer/measure entanglement properties of target quantum states. In this work, we extend the use of SNNS to mixed, multipartite states, providing a versatile and efficient tool for the investigation of intricately entangled quantum systems. We illustrate the effectiveness of our method through a number of examples, such as the computation of novel tripartite entanglement measures, and the approximation of ultimate upper bounds for qudit channel capacities.