Why Not? Explaining Missing Entailments with Evee (Technical Report)

Understanding logical entailments derived by a description logic reasoner is not always straight-forward for ontology users. For this reason, various methods for explaining entailments using justifications and proofs have been developed and implemented as plug-ins for the ontology editor Prot\'eg\'e. However, when the user expects a missing consequence to hold, it is equally important to explain why it does not follow from the ontology. In this paper, we describe a new version of $\rm E{\scriptsize VEE}$, a Prot\'eg\'e plugin that now also provides explanations for missing consequences, via existing and new techniques based on abduction and counterexamples.

On the Eve of True Explainability for OWL Ontologies: Description Logic Proofs with Evee and Evonne

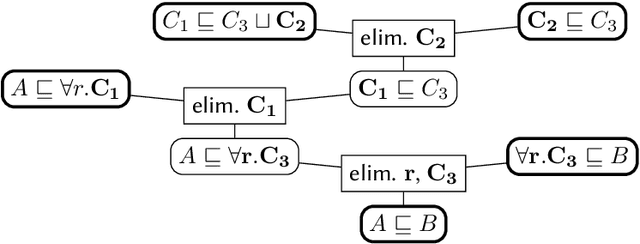
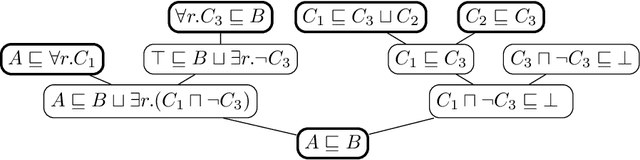
When working with description logic ontologies, understanding entailments derived by a description logic reasoner is not always straightforward. So far, the standard ontology editor Prot\'eg\'e offers two services to help: (black-box) justifications for OWL 2 DL ontologies, and (glass-box) proofs for lightweight OWL EL ontologies, where the latter exploits the proof facilities of reasoner ELK. Since justifications are often insufficient in explaining inferences, there is thus only little tool support for explaining inferences in more expressive DLs. In this paper, we introduce EVEE-LIBS, a Java library for computing proofs for DLs up to ALCH, and EVEE-PROTEGE, a collection of Prot\'eg\'e plugins for displaying those proofs in Prot\'eg\'e. We also give a short glimpse of the latest version of EVONNE, a more advanced standalone application for displaying and interacting with proofs computed with EVEE-LIBS.

Evonne: Interactive Proof Visualization for Description Logics (System Description) -- Extended Version

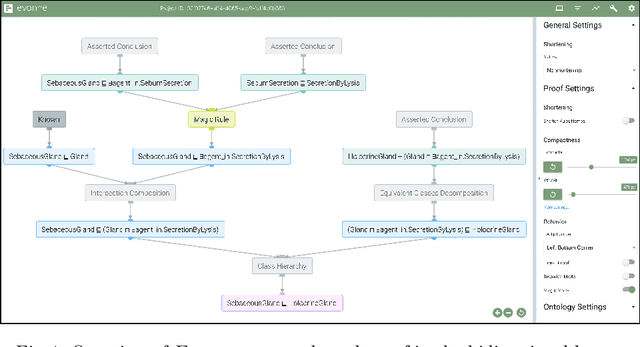
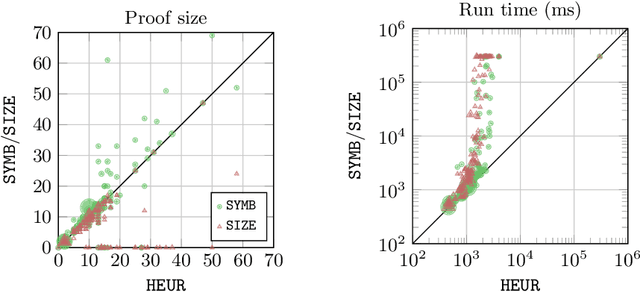
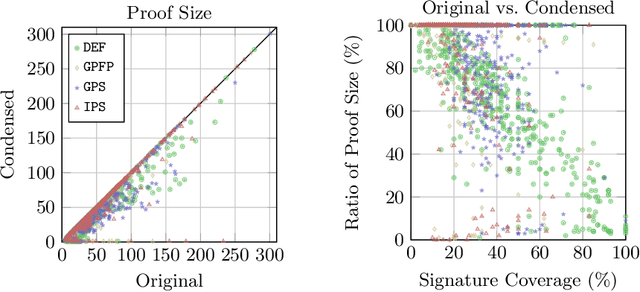
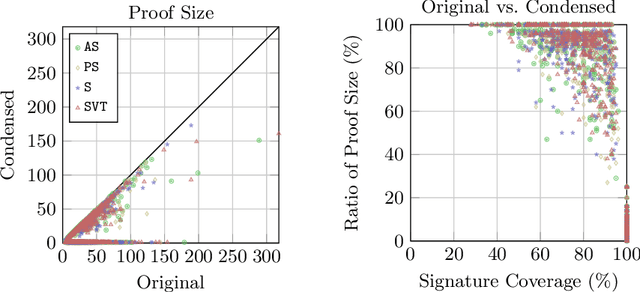
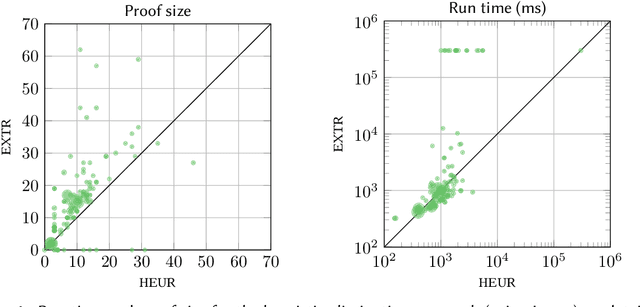
Explanations for description logic (DL) entailments provide important support for the maintenance of large ontologies. The "justifications" usually employed for this purpose in ontology editors pinpoint the parts of the ontology responsible for a given entailment. Proofs for entailments make the intermediate reasoning steps explicit, and thus explain how a consequence can actually be derived. We present an interactive system for exploring description logic proofs, called Evonne, which visualizes proofs of consequences for ontologies written in expressive DLs. We describe the methods used for computing those proofs, together with a feature called signature-based proof condensation. Moreover, we evaluate the quality of generated proofs using real ontologies.

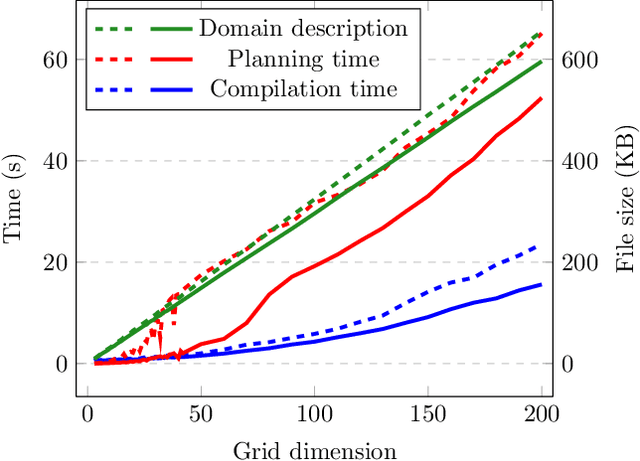
Expressivity of Planning with Horn Description Logic Ontologies (Technical Report)

State constraints in AI Planning globally restrict the legal environment states. Standard planning languages make closed-domain and closed-world assumptions. Here we address open-world state constraints formalized by planning over a description logic (DL) ontology. Previously, this combination of DL and planning has been investigated for the light-weight DL DL-Lite. Here we propose a novel compilation scheme into standard PDDL with derived predicates, which applies to more expressive DLs and is based on the rewritability of DL queries into Datalog with stratified negation. We also provide a new rewritability result for the DL Horn-ALCHOIQ, which allows us to apply our compilation scheme to quite expressive ontologies. In contrast, we show that in the slight extension Horn-SROIQ no such compilation is possible unless the weak exponential hierarchy collapses. Finally, we show that our approach can outperform previous work on existing benchmarks for planning with DL ontologies, and is feasible on new benchmarks taking advantage of more expressive ontologies. That is an extended version of a paper accepted at AAAI 22.

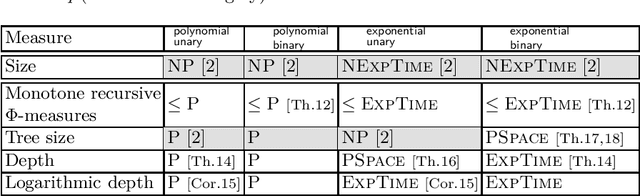
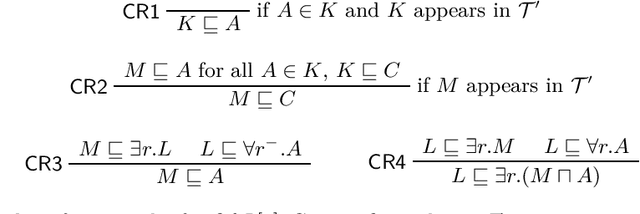
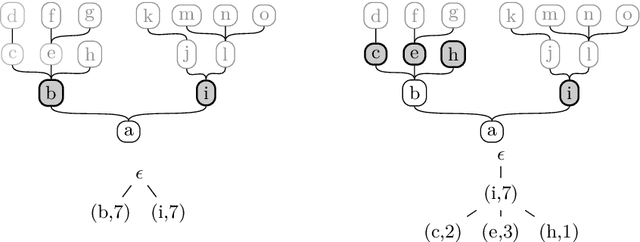
Finding Good Proofs for Description Logic Entailments Using Recursive Quality Measures (Extended Technical Report)

Logic-based approaches to AI have the advantage that their behavior can in principle be explained to a user. If, for instance, a Description Logic reasoner derives a consequence that triggers some action of the overall system, then one can explain such an entailment by presenting a proof of the consequence in an appropriate calculus. How comprehensible such a proof is depends not only on the employed calculus, but also on the properties of the particular proof, such as its overall size, its depth, the complexity of the employed sentences and proof steps, etc. For this reason, we want to determine the complexity of generating proofs that are below a certain threshold w.r.t. a given measure of proof quality. Rather than investigating this problem for a fixed proof calculus and a fixed measure, we aim for general results that hold for wide classes of calculi and measures. In previous work, we first restricted the attention to a setting where proof size is used to measure the quality of a proof. We then extended the approach to a more general setting, but important measures such as proof depth were not covered. In the present paper, we provide results for a class of measures called recursive, which yields lower complexities and also encompasses proof depth. In addition, we close some gaps left open in our previous work, thus providing a comprehensive picture of the complexity landscape.

Extending Unification in $\mathcal{EL}$ to Disunification: The Case of Dismatching and Local Disunification

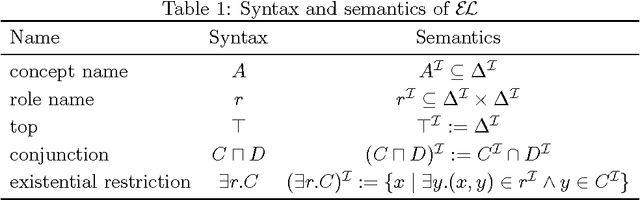
Unification in Description Logics has been introduced as a means to detect redundancies in ontologies. We try to extend the known decidability results for unification in the Description Logic $\mathcal{EL}$ to disunification since negative constraints can be used to avoid unwanted unifiers. While decidability of the solvability of general $\mathcal{EL}$-disunification problems remains an open problem, we obtain NP-completeness results for two interesting special cases: dismatching problems, where one side of each negative constraint must be ground, and local solvability of disunification problems, where we consider only solutions that are constructed from terms occurring in the input problem. More precisely, we first show that dismatching can be reduced to local disunification, and then provide two complementary NP-algorithms for finding local solutions of disunification problems.

Answering Fuzzy Conjunctive Queries over Finitely Valued Fuzzy Ontologies

Fuzzy Description Logics (DLs) provide a means for representing vague knowledge about an application domain. In this paper, we study fuzzy extensions of conjunctive queries (CQs) over the DL $\mathcal{SROIQ}$ based on finite chains of degrees of truth. To answer such queries, we extend a well-known technique that reduces the fuzzy ontology to a classical one, and use classical DL reasoners as a black box. We improve the complexity of previous reduction techniques for finitely valued fuzzy DLs, which allows us to prove tight complexity results for answering certain kinds of fuzzy CQs. We conclude with an experimental evaluation of a prototype implementation, showing the feasibility of our approach.

Reasoning in Infinitely Valued G-IALCQ

Fuzzy Description Logics (FDLs) are logic-based formalisms used to represent and reason with vague or imprecise knowledge. It has been recently shown that reasoning in most FDLs using truth values from the interval [0,1] becomes undecidable in the presence of a negation constructor and general concept inclusion axioms. One exception to this negative result are FDLs whose semantics is based on the infinitely valued G\"odel t-norm (G). In this paper, we extend previous decidability results for G-IALC to deal also with qualified number restrictions. Our novel approach is based on a combination of the known crispification technique for finitely valued FDLs and the automata-based procedure originally developed for reasoning in G-IALC. The proposed approach combines the advantages of these two methods, while removing their respective drawbacks.