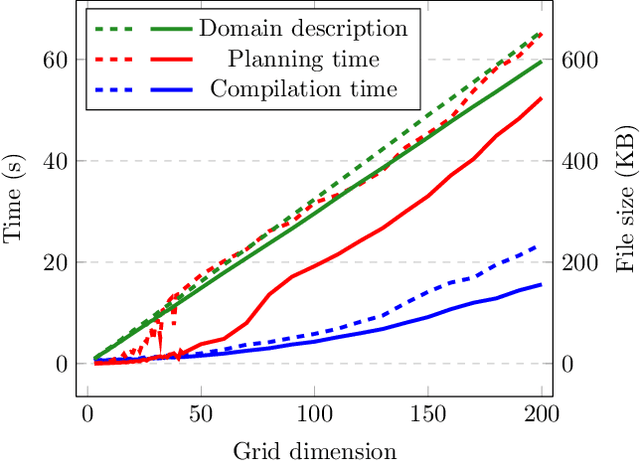
Expressivity of Planning with Horn Description Logic Ontologies (Technical Report)

State constraints in AI Planning globally restrict the legal environment states. Standard planning languages make closed-domain and closed-world assumptions. Here we address open-world state constraints formalized by planning over a description logic (DL) ontology. Previously, this combination of DL and planning has been investigated for the light-weight DL DL-Lite. Here we propose a novel compilation scheme into standard PDDL with derived predicates, which applies to more expressive DLs and is based on the rewritability of DL queries into Datalog with stratified negation. We also provide a new rewritability result for the DL Horn-ALCHOIQ, which allows us to apply our compilation scheme to quite expressive ontologies. In contrast, we show that in the slight extension Horn-SROIQ no such compilation is possible unless the weak exponential hierarchy collapses. Finally, we show that our approach can outperform previous work on existing benchmarks for planning with DL ontologies, and is feasible on new benchmarks taking advantage of more expressive ontologies. That is an extended version of a paper accepted at AAAI 22.

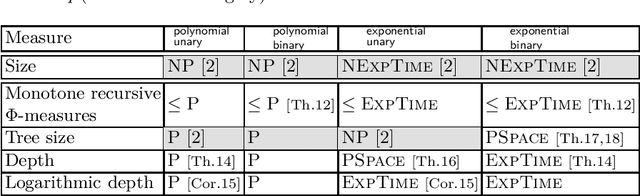
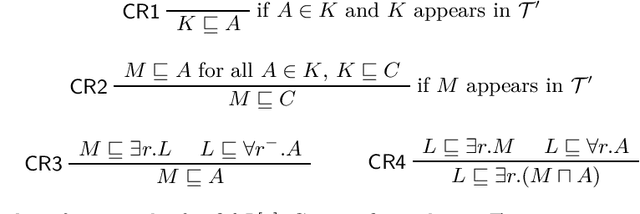
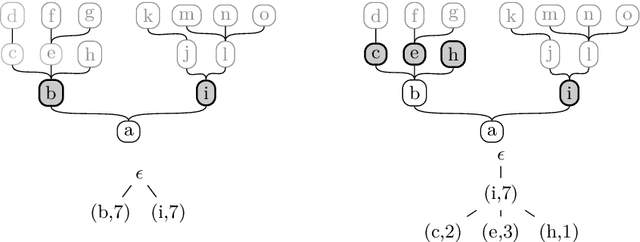
Finding Good Proofs for Description Logic Entailments Using Recursive Quality Measures (Extended Technical Report)

Logic-based approaches to AI have the advantage that their behavior can in principle be explained to a user. If, for instance, a Description Logic reasoner derives a consequence that triggers some action of the overall system, then one can explain such an entailment by presenting a proof of the consequence in an appropriate calculus. How comprehensible such a proof is depends not only on the employed calculus, but also on the properties of the particular proof, such as its overall size, its depth, the complexity of the employed sentences and proof steps, etc. For this reason, we want to determine the complexity of generating proofs that are below a certain threshold w.r.t. a given measure of proof quality. Rather than investigating this problem for a fixed proof calculus and a fixed measure, we aim for general results that hold for wide classes of calculi and measures. In previous work, we first restricted the attention to a setting where proof size is used to measure the quality of a proof. We then extended the approach to a more general setting, but important measures such as proof depth were not covered. In the present paper, we provide results for a class of measures called recursive, which yields lower complexities and also encompasses proof depth. In addition, we close some gaps left open in our previous work, thus providing a comprehensive picture of the complexity landscape.