On the Computational Complexity of Stackelberg Planning and Meta-Operator Verification: Technical Report

Stackelberg planning is a recently introduced single-turn two-player adversarial planning model, where two players are acting in a joint classical planning task, the objective of the first player being hampering the second player from achieving its goal. This places the Stackelberg planning problem somewhere between classical planning and general combinatorial two-player games. But, where exactly? All investigations of Stackelberg planning so far focused on practical aspects. We close this gap by conducting the first theoretical complexity analysis of Stackelberg planning. We show that in general Stackelberg planning is actually no harder than classical planning. Under a polynomial plan-length restriction, however, Stackelberg planning is a level higher up in the polynomial complexity hierarchy, suggesting that compilations into classical planning come with a worst-case exponential plan-length increase. In attempts to identify tractable fragments, we further study its complexity under various planning task restrictions, showing that Stackelberg planning remains intractable where classical planning is not. We finally inspect the complexity of meta-operator verification, a problem that has been recently connected to Stackelberg planning.

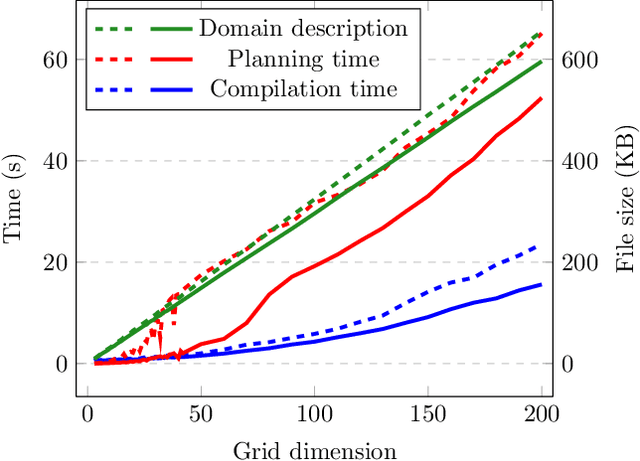
Expressivity of Planning with Horn Description Logic Ontologies (Technical Report)

State constraints in AI Planning globally restrict the legal environment states. Standard planning languages make closed-domain and closed-world assumptions. Here we address open-world state constraints formalized by planning over a description logic (DL) ontology. Previously, this combination of DL and planning has been investigated for the light-weight DL DL-Lite. Here we propose a novel compilation scheme into standard PDDL with derived predicates, which applies to more expressive DLs and is based on the rewritability of DL queries into Datalog with stratified negation. We also provide a new rewritability result for the DL Horn-ALCHOIQ, which allows us to apply our compilation scheme to quite expressive ontologies. In contrast, we show that in the slight extension Horn-SROIQ no such compilation is possible unless the weak exponential hierarchy collapses. Finally, we show that our approach can outperform previous work on existing benchmarks for planning with DL ontologies, and is feasible on new benchmarks taking advantage of more expressive ontologies. That is an extended version of a paper accepted at AAAI 22.

Simulated Penetration Testing and Mitigation Analysis

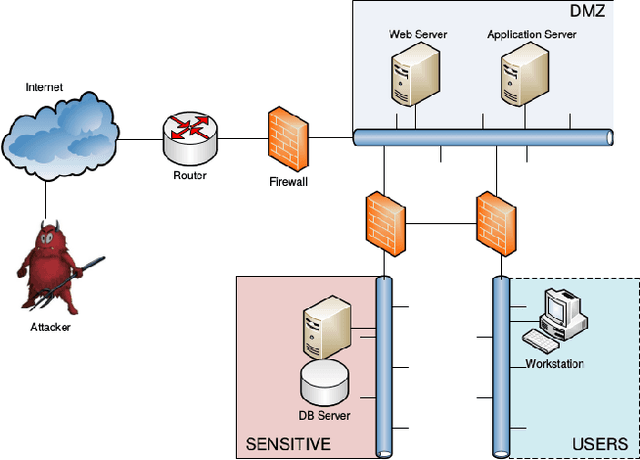
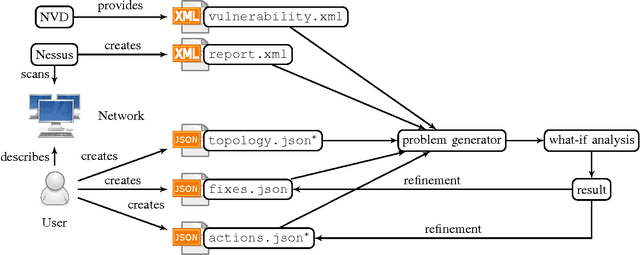
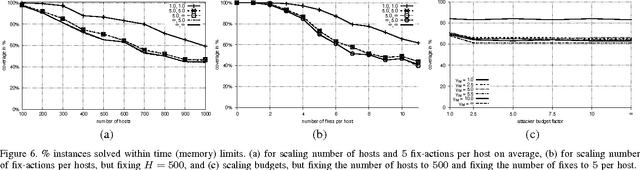
Penetration testing is a well-established practical concept for the identification of potentially exploitable security weaknesses and an important component of a security audit. Providing a holistic security assessment for networks consisting of several hundreds hosts is hardly feasible though without some sort of mechanization. Mitigation, prioritizing counter- measures subject to a given budget, currently lacks a solid theoretical understanding and is hence more art than science. In this work, we propose the first approach for conduct- ing comprehensive what-if analyses in order to reason about mitigation in a conceptually well-founded manner. To evaluate and compare mitigation strategies, we use simulated penetration testing, i.e., automated attack-finding, based on a network model to which a subset of a given set of mitigation actions, e.g., changes to the network topology, system updates, configuration changes etc. is applied. We determine optimal combinations that minimize the maximal attacker success (similar to a Stackelberg game), and thus provide a well-founded basis for a holistic mitigation strategy. We show that these what-if analysis models can largely be derived from network scan, public vulnerability databases and manual inspection with various degrees of automation and detail, and we simulate mitigation analysis on networks of different size and vulnerability.