Interpolation in Knowledge Representation

Craig interpolation and uniform interpolation have many applications in knowledge representation, including explainability, forgetting, modularization and reuse, and even learning. At the same time, many relevant knowledge representation formalisms do in general not have Craig or uniform interpolation, and computing interpolants in practice is challenging. We have a closer look at two prominent knowledge representation formalisms, description logics and logic programming, and discuss theoretical results and practical methods for computing interpolants.

Can You Tell the Difference? Contrastive Explanations for ABox Entailments

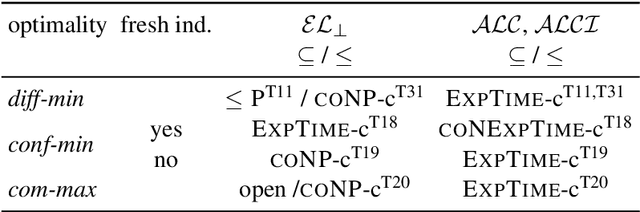
We introduce the notion of contrastive ABox explanations to answer questions of the type "Why is a an instance of C, but b is not?". While there are various approaches for explaining positive entailments (why is C(a) entailed by the knowledge base) as well as missing entailments (why is C(b) not entailed) in isolation, contrastive explanations consider both at the same time, which allows them to focus on the relevant commonalities and differences between a and b. We develop an appropriate notion of contrastive explanations for the special case of ABox reasoning with description logic ontologies, and analyze the computational complexity for different variants under different optimality criteria, considering lightweight as well as more expressive description logics. We implemented a first method for computing one variant of contrastive explanations, and evaluated it on generated problems for realistic knowledge bases.

Planning with OWL-DL Ontologies (Extended Version)

We introduce ontology-mediated planning, in which planning problems are combined with an ontology. Our formalism differs from existing ones in that we focus on a strong separation of the formalisms for describing planning problems and ontologies, which are only losely coupled by an interface. Moreover, we present a black-box algorithm that supports the full expressive power of OWL DL. This goes beyond what existing approaches combining automated planning with ontologies can do, which only support limited description logics such as DL-Lite and description logics that are Horn. Our main algorithm relies on rewritings of the ontology-mediated planning specifications into PDDL, so that existing planning systems can be used to solve them. The algorithm relies on justifications, which allows for a generic approach that is independent of the expressivity of the ontology language. However, dedicated optimizations for computing justifications need to be implemented to enable an efficient rewriting procedure. We evaluated our implementation on benchmark sets from several domains. The evaluation shows that our procedure works in practice and that tailoring the reasoning procedure has significant impact on the performance.

Towards Ontology-Mediated Planning with OWL DL Ontologies (Extended Version)

While classical planning languages make the closed-domain and closed-world assumption, there have been various approaches to extend those with DL reasoning, which is then interpreted under the usual open-world semantics. Current approaches for planning with DL ontologies integrate the DL directly into the planning language, and practical approaches have been developed based on first-order rewritings or rewritings into datalog. We present here a new approach in which the planning specification and ontology are kept separate, and are linked together using an interface. This allows planning experts to work in a familiar formalism, while existing ontologies can be easily integrated and extended by ontology experts. Our approach for planning with those ontology-mediated planning problems is optimized for cases with comparatively small domains, and supports the whole OWL DL fragment. The idea is to rewrite the ontology-mediated planning problem into a classical planning problem to be processed by existing planning tools. Different to other approaches, our rewriting is data-dependent. A first experimental evaluation of our approach shows the potential and limitations of this approach.

Why Not? Explaining Missing Entailments with Evee (Technical Report)

Understanding logical entailments derived by a description logic reasoner is not always straight-forward for ontology users. For this reason, various methods for explaining entailments using justifications and proofs have been developed and implemented as plug-ins for the ontology editor Prot\'eg\'e. However, when the user expects a missing consequence to hold, it is equally important to explain why it does not follow from the ontology. In this paper, we describe a new version of $\rm E{\scriptsize VEE}$, a Prot\'eg\'e plugin that now also provides explanations for missing consequences, via existing and new techniques based on abduction and counterexamples.

Efficient Computation of General Modules for ALC Ontologies (Extended Version)

We present a method for extracting general modules for ontologies formulated in the description logic ALC. A module for an ontology is an ideally substantially smaller ontology that preserves all entailments for a user-specified set of terms. As such, it has applications such as ontology reuse and ontology analysis. Different from classical modules, general modules may use axioms not explicitly present in the input ontology, which allows for additional conciseness. So far, general modules have only been investigated for lightweight description logics. We present the first work that considers the more expressive description logic ALC. In particular, our contribution is a new method based on uniform interpolation supported by some new theoretical results. Our evaluation indicates that our general modules are often smaller than classical modules and uniform interpolants computed by the state-of-the-art, and compared with uniform interpolants, can be computed in a significantly shorter time. Moreover, our method can be used for, and in fact improves, the computation of uniform interpolants and classical modules.

On the Eve of True Explainability for OWL Ontologies: Description Logic Proofs with Evee and Evonne

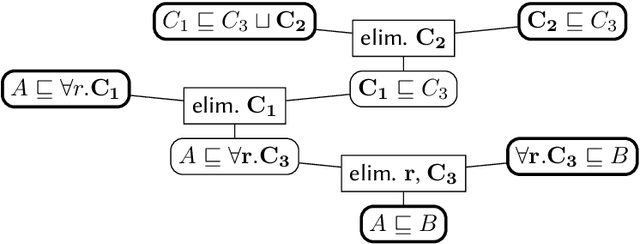
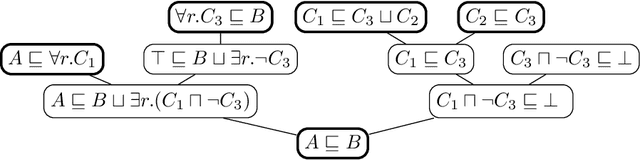
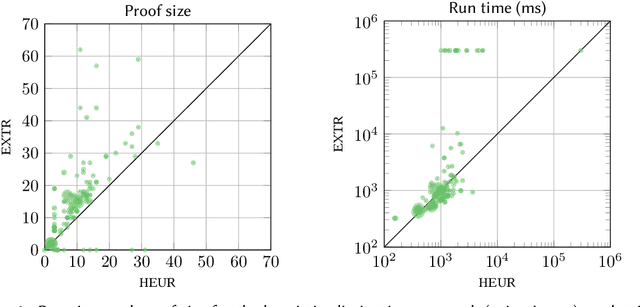
When working with description logic ontologies, understanding entailments derived by a description logic reasoner is not always straightforward. So far, the standard ontology editor Prot\'eg\'e offers two services to help: (black-box) justifications for OWL 2 DL ontologies, and (glass-box) proofs for lightweight OWL EL ontologies, where the latter exploits the proof facilities of reasoner ELK. Since justifications are often insufficient in explaining inferences, there is thus only little tool support for explaining inferences in more expressive DLs. In this paper, we introduce EVEE-LIBS, a Java library for computing proofs for DLs up to ALCH, and EVEE-PROTEGE, a collection of Prot\'eg\'e plugins for displaying those proofs in Prot\'eg\'e. We also give a short glimpse of the latest version of EVONNE, a more advanced standalone application for displaying and interacting with proofs computed with EVEE-LIBS.

Connection-minimal Abduction in EL via Translation to FOL -- Technical Report

Abduction in description logics finds extensions of a knowledge base to make it entail an observation. As such, it can be used to explain why the observation does not follow, to repair incomplete knowledge bases, and to provide possible explanations for unexpected observations. We consider TBox abduction in the lightweight description logic EL, where the observation is a concept inclusion and the background knowledge is a TBox, i.e., a set of concept inclusions. To avoid useless answers, such problems usually come with further restrictions on the solution space and/or minimality criteria that help sort the chaff from the grain. We argue that existing minimality notions are insufficient, and introduce connection minimality. This criterion follows Occam's razor by rejecting hypotheses that use concept inclusions unrelated to the problem at hand. We show how to compute a special class of connection-minimal hypotheses in a sound and complete way. Our technique is based on a translation to first-order logic, and constructs hypotheses based on prime implicates. We evaluate a prototype implementation of our approach on ontologies from the medical domain.

Evonne: Interactive Proof Visualization for Description Logics (System Description) -- Extended Version

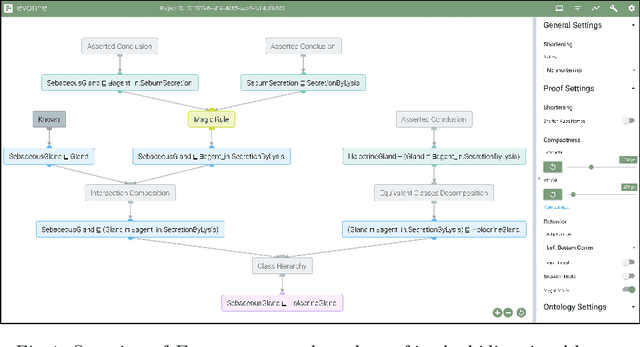
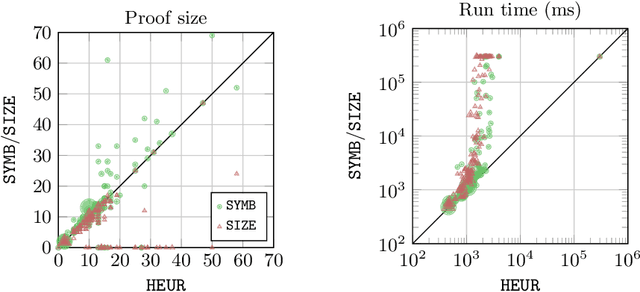
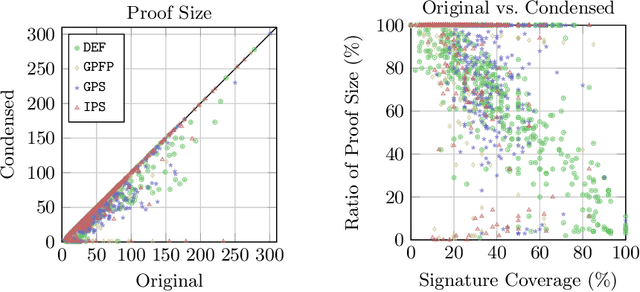
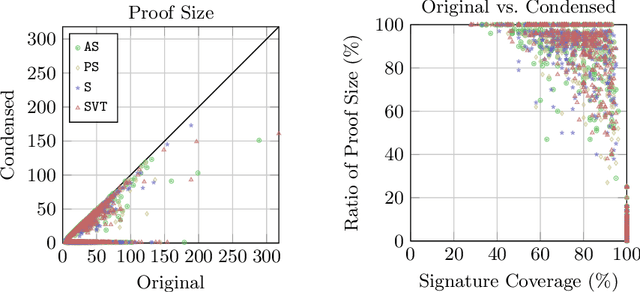
Explanations for description logic (DL) entailments provide important support for the maintenance of large ontologies. The "justifications" usually employed for this purpose in ontology editors pinpoint the parts of the ontology responsible for a given entailment. Proofs for entailments make the intermediate reasoning steps explicit, and thus explain how a consequence can actually be derived. We present an interactive system for exploring description logic proofs, called Evonne, which visualizes proofs of consequences for ontologies written in expressive DLs. We describe the methods used for computing those proofs, together with a feature called signature-based proof condensation. Moreover, we evaluate the quality of generated proofs using real ontologies.

Efficient TBox Reasoning with Value Restrictions using the $\mathcal{FL}_{o}$wer reasoner

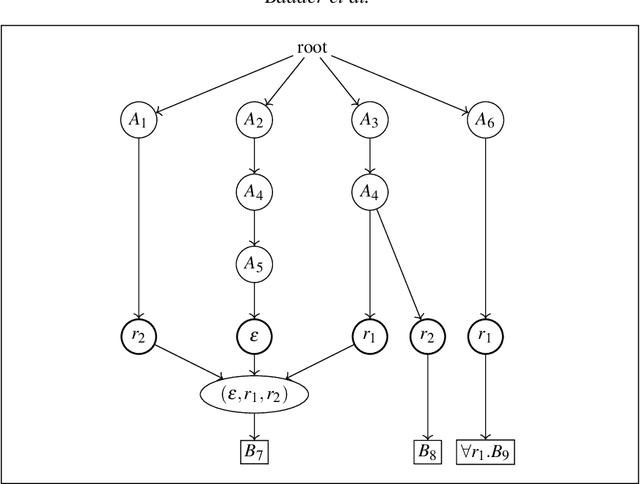
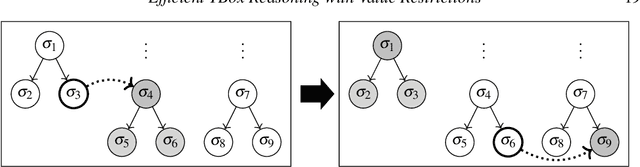
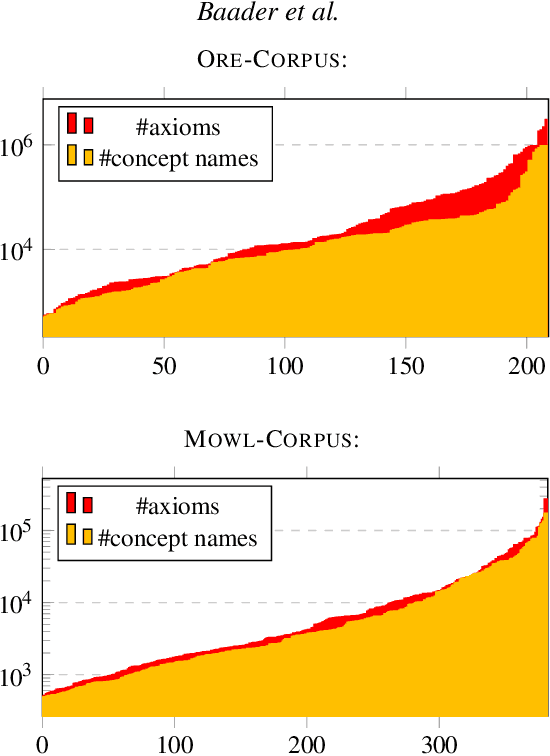
The inexpressive Description Logic (DL) $\mathcal{FL}_0$, which has conjunction and value restriction as its only concept constructors, had fallen into disrepute when it turned out that reasoning in $\mathcal{FL}_0$ w.r.t. general TBoxes is ExpTime-complete, i.e., as hard as in the considerably more expressive logic $\mathcal{ALC}$. In this paper, we rehabilitate $\mathcal{FL}_0$ by presenting a dedicated subsumption algorithm for $\mathcal{FL}_0$, which is much simpler than the tableau-based algorithms employed by highly optimized DL reasoners. Our experiments show that the performance of our novel algorithm, as prototypically implemented in our $\mathcal{FL}_o$wer reasoner, compares very well with that of the highly optimized reasoners. $\mathcal{FL}_o$wer can also deal with ontologies written in the extension $\mathcal{FL}_{\bot}$ of $\mathcal{FL}_0$ with the top and the bottom concept by employing a polynomial-time reduction, shown in this paper, which eliminates top and bottom. We also investigate the complexity of reasoning in DLs related to the Horn-fragments of $\mathcal{FL}_0$ and $\mathcal{FL}_{\bot}$.