Connection-minimal Abduction in EL via Translation to FOL -- Technical Report

Abduction in description logics finds extensions of a knowledge base to make it entail an observation. As such, it can be used to explain why the observation does not follow, to repair incomplete knowledge bases, and to provide possible explanations for unexpected observations. We consider TBox abduction in the lightweight description logic EL, where the observation is a concept inclusion and the background knowledge is a TBox, i.e., a set of concept inclusions. To avoid useless answers, such problems usually come with further restrictions on the solution space and/or minimality criteria that help sort the chaff from the grain. We argue that existing minimality notions are insufficient, and introduce connection minimality. This criterion follows Occam's razor by rejecting hypotheses that use concept inclusions unrelated to the problem at hand. We show how to compute a special class of connection-minimal hypotheses in a sound and complete way. Our technique is based on a translation to first-order logic, and constructs hypotheses based on prime implicates. We evaluate a prototype implementation of our approach on ontologies from the medical domain.

Superposition with Lambdas

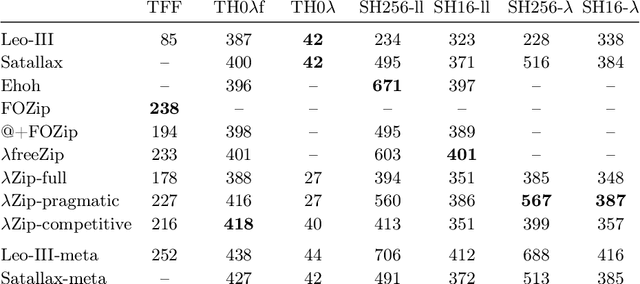
We designed a superposition calculus for a clausal fragment of extensional polymorphic higher-order logic that includes anonymous functions but excludes Booleans. The inference rules work on $\beta\eta$-equivalence classes of $\lambda$-terms and rely on higher-order unification to achieve refutational completeness. We implemented the calculus in the Zipperposition prover and evaluated it on TPTP and Isabelle benchmarks. The results suggest that superposition is a suitable basis for higher-order reasoning.

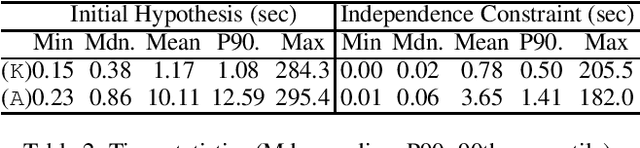
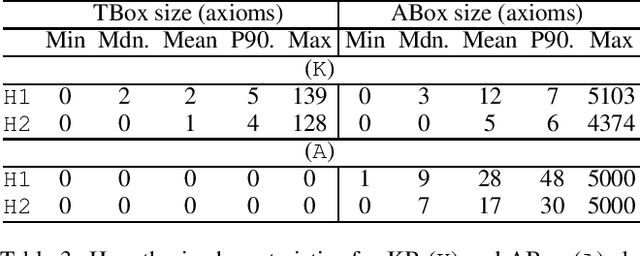
Signature-Based Abduction for Expressive Description Logics -- Technical Report

Signature-based abduction aims at building hypotheses over a specified set of names, the signature, that explain an observation relative to some background knowledge. This type of abduction is useful for tasks such as diagnosis, where the vocabulary used for observed symptoms differs from the vocabulary expected to explain those symptoms. We present the first complete method solving signature-based abduction for observations expressed in the expressive description logic ALC, which can include TBox and ABox axioms, thereby solving the knowledge base abduction problem. The method is guaranteed to compute a finite and complete set of hypotheses, and is evaluated on a set of realistic knowledge bases.

Logical reduction of metarules

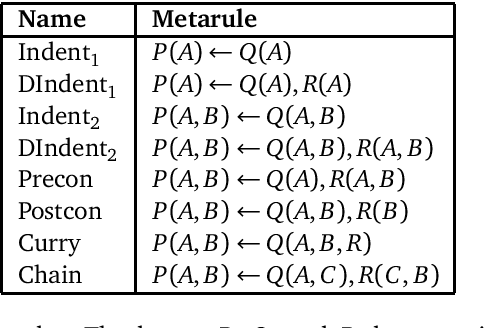
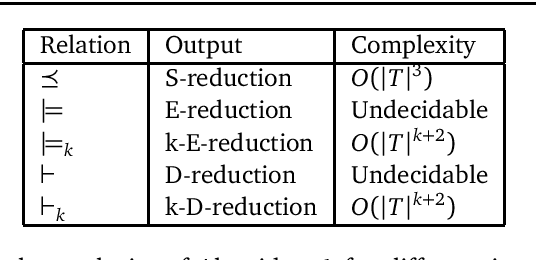
Many forms of inductive logic programming (ILP) use \emph{metarules}, second-order Horn clauses, to define the structure of learnable programs and thus the hypothesis space. Deciding which metarules to use for a given learning task is a major open problem and is a trade-off between efficiency and expressivity: the hypothesis space grows given more metarules, so we wish to use fewer metarules, but if we use too few metarules then we lose expressivity. In this paper, we study whether fragments of metarules can be logically reduced to minimal finite subsets. We consider two traditional forms of logical reduction: subsumption and entailment. We also consider a new reduction technique called \emph{derivation reduction}, which is based on SLD-resolution. We compute reduced sets of metarules for fragments relevant to ILP and theoretically show whether these reduced sets are reductions for more general infinite fragments. We experimentally compare learning with reduced sets of metarules on three domains: Michalski trains, string transformations, and game rules. In general, derivation reduced sets of metarules outperforms subsumption and entailment reduced sets, both in terms of predictive accuracies and learning times.