Logical reduction of metarules
Paper and Code
Jul 25, 2019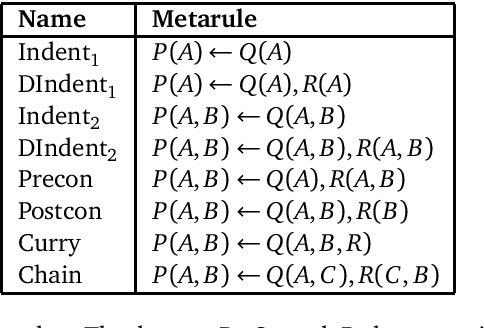

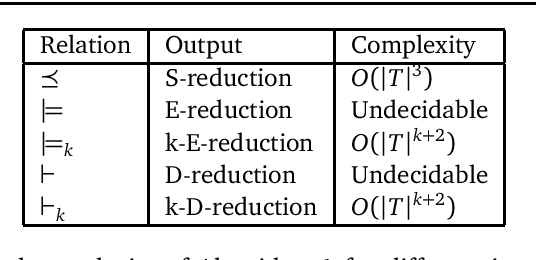

Many forms of inductive logic programming (ILP) use \emph{metarules}, second-order Horn clauses, to define the structure of learnable programs and thus the hypothesis space. Deciding which metarules to use for a given learning task is a major open problem and is a trade-off between efficiency and expressivity: the hypothesis space grows given more metarules, so we wish to use fewer metarules, but if we use too few metarules then we lose expressivity. In this paper, we study whether fragments of metarules can be logically reduced to minimal finite subsets. We consider two traditional forms of logical reduction: subsumption and entailment. We also consider a new reduction technique called \emph{derivation reduction}, which is based on SLD-resolution. We compute reduced sets of metarules for fragments relevant to ILP and theoretically show whether these reduced sets are reductions for more general infinite fragments. We experimentally compare learning with reduced sets of metarules on three domains: Michalski trains, string transformations, and game rules. In general, derivation reduced sets of metarules outperforms subsumption and entailment reduced sets, both in terms of predictive accuracies and learning times.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge