The More the Merrier: Combining Properties for ABox Abduction under Repair Semantics for ELbot

Abduction is a central approach to explain missing entailments from a knowledge base by providing a hypothesis, that would, if added to the knowledge base, make the missing entailment become true. Abduction under repair semantics has recently been investigated in detail, where several desirable properties and optimality criteria were considered, such as signature-restrictions and minimality in size and of introduced conflicts. Naturally, hypotheses that satisfy more than one of these properties or combine a property with an optimality criterion would be even more desirable for applications. So far, such hypotheses have not been investigated in the literature. In the present paper, we consider the ABox abduction problem for hypotheses satisfying more than one property or additional optimality criteria, for EL_bot under brave and AR semantics. Our main observation is that often requiring additional properties for hypotheses does not lead to an increase of complexity.

Optimal Alignment of Temporal Knowledge Bases

Answering temporal CQs over temporalized Description Logic knowledge bases (TKB) is a main technique to realize ontology-based situation recognition. In case the collected data in such a knowledge base is inaccurate, important query answers can be missed. In this paper we introduce the TKB Alignment problem, which computes a variant of the TKB that minimally changes the TKB, but entails the given temporal CQ and is in that sense (cost-)optimal. We investigate this problem for ALC TKBs and conjunctive queries with LTL operators and devise a solution technique to compute (cost-optimal) alignments of TKBs that extends techniques for the alignment problem for propositional LTL over finite traces.

Efficient TBox Reasoning with Value Restrictions using the $\mathcal{FL}_{o}$wer reasoner

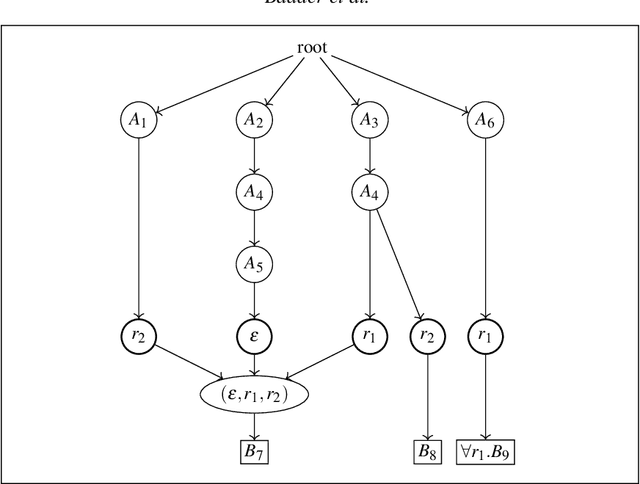
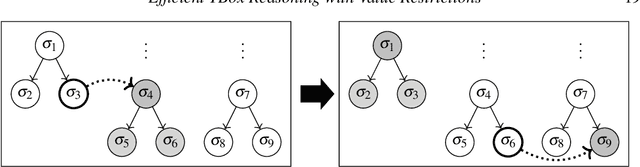
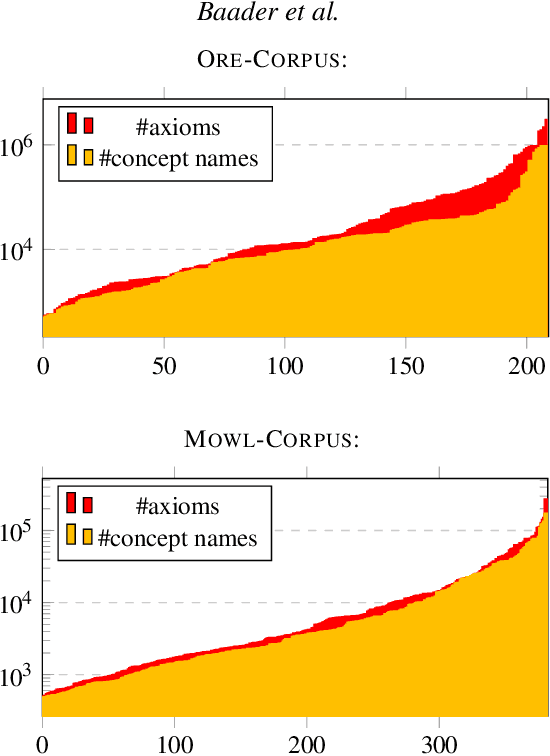
The inexpressive Description Logic (DL) $\mathcal{FL}_0$, which has conjunction and value restriction as its only concept constructors, had fallen into disrepute when it turned out that reasoning in $\mathcal{FL}_0$ w.r.t. general TBoxes is ExpTime-complete, i.e., as hard as in the considerably more expressive logic $\mathcal{ALC}$. In this paper, we rehabilitate $\mathcal{FL}_0$ by presenting a dedicated subsumption algorithm for $\mathcal{FL}_0$, which is much simpler than the tableau-based algorithms employed by highly optimized DL reasoners. Our experiments show that the performance of our novel algorithm, as prototypically implemented in our $\mathcal{FL}_o$wer reasoner, compares very well with that of the highly optimized reasoners. $\mathcal{FL}_o$wer can also deal with ontologies written in the extension $\mathcal{FL}_{\bot}$ of $\mathcal{FL}_0$ with the top and the bottom concept by employing a polynomial-time reduction, shown in this paper, which eliminates top and bottom. We also investigate the complexity of reasoning in DLs related to the Horn-fragments of $\mathcal{FL}_0$ and $\mathcal{FL}_{\bot}$.

Answering Fuzzy Conjunctive Queries over Finitely Valued Fuzzy Ontologies

Fuzzy Description Logics (DLs) provide a means for representing vague knowledge about an application domain. In this paper, we study fuzzy extensions of conjunctive queries (CQs) over the DL $\mathcal{SROIQ}$ based on finite chains of degrees of truth. To answer such queries, we extend a well-known technique that reduces the fuzzy ontology to a classical one, and use classical DL reasoners as a black box. We improve the complexity of previous reduction techniques for finitely valued fuzzy DLs, which allows us to prove tight complexity results for answering certain kinds of fuzzy CQs. We conclude with an experimental evaluation of a prototype implementation, showing the feasibility of our approach.