Extending Unification in $\mathcal{EL}$ to Disunification: The Case of Dismatching and Local Disunification

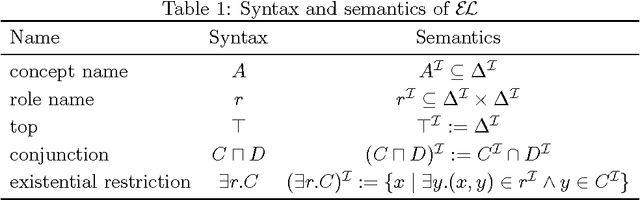
Unification in Description Logics has been introduced as a means to detect redundancies in ontologies. We try to extend the known decidability results for unification in the Description Logic $\mathcal{EL}$ to disunification since negative constraints can be used to avoid unwanted unifiers. While decidability of the solvability of general $\mathcal{EL}$-disunification problems remains an open problem, we obtain NP-completeness results for two interesting special cases: dismatching problems, where one side of each negative constraint must be ground, and local solvability of disunification problems, where we consider only solutions that are constructed from terms occurring in the input problem. More precisely, we first show that dismatching can be reduced to local disunification, and then provide two complementary NP-algorithms for finding local solutions of disunification problems.

Unification in the Description Logic EL

The Description Logic EL has recently drawn considerable attention since, on the one hand, important inference problems such as the subsumption problem are polynomial. On the other hand, EL is used to define large biomedical ontologies. Unification in Description Logics has been proposed as a novel inference service that can, for example, be used to detect redundancies in ontologies. The main result of this paper is that unification in EL is decidable. More precisely, EL-unification is NP-complete, and thus has the same complexity as EL-matching. We also show that, w.r.t. the unification type, EL is less well-behaved: it is of type zero, which in particular implies that there are unification problems that have no finite complete set of unifiers.