AI-generated data contamination erodes pathological variability and diagnostic reliability

Generative artificial intelligence (AI) is rapidly populating medical records with synthetic content, creating a feedback loop where future models are increasingly at risk of training on uncurated AI-generated data. However, the clinical consequences of this AI-generated data contamination remain unexplored. Here, we show that in the absence of mandatory human verification, this self-referential cycle drives a rapid erosion of pathological variability and diagnostic reliability. By analysing more than 800,000 synthetic data points across clinical text generation, vision-language reporting, and medical image synthesis, we find that models progressively converge toward generic phenotypes regardless of the model architecture. Specifically, rare but critical findings, including pneumothorax and effusions, vanish from the synthetic content generated by AI models, while demographic representations skew heavily toward middle-aged male phenotypes. Crucially, this degradation is masked by false diagnostic confidence; models continue to issue reassuring reports while failing to detect life-threatening pathology, with false reassurance rates tripling to 40%. Blinded physician evaluation confirms that this decoupling of confidence and accuracy renders AI-generated documentation clinically useless after just two generations. We systematically evaluate three mitigation strategies, finding that while synthetic volume scaling fails to prevent collapse, mixing real data with quality-aware filtering effectively preserves diversity. Ultimately, our results suggest that without policy-mandated human oversight, the deployment of generative AI threatens to degrade the very healthcare data ecosystems it relies upon.

Laplacian Score Sharpening for Mitigating Hallucination in Diffusion Models

Diffusion models, though successful, are known to suffer from hallucinations that create incoherent or unrealistic samples. Recent works have attributed this to the phenomenon of mode interpolation and score smoothening, but they lack a method to prevent their generation during sampling. In this paper, we propose a post-hoc adjustment to the score function during inference that leverages the Laplacian (or sharpness) of the score to reduce mode interpolation hallucination in unconditional diffusion models across 1D, 2D, and high-dimensional image data. We derive an efficient Laplacian approximation for higher dimensions using a finite-difference variant of the Hutchinson trace estimator. We show that this correction significantly reduces the rate of hallucinated samples across toy 1D/2D distributions and a high-dimensional image dataset. Furthermore, our analysis explores the relationship between the Laplacian and uncertainty in the score.

Auto-Bench: An Automated Benchmark for Scientific Discovery in LLMs

Given the remarkable performance of Large Language Models (LLMs), an important question arises: Can LLMs conduct human-like scientific research and discover new knowledge, and act as an AI scientist? Scientific discovery is an iterative process that demands efficient knowledge updating and encoding. It involves understanding the environment, identifying new hypotheses, and reasoning about actions; however, no standardized benchmark specifically designed for scientific discovery exists for LLM agents. In response to these limitations, we introduce a novel benchmark, \textit{Auto-Bench}, that encompasses necessary aspects to evaluate LLMs for scientific discovery in both natural and social sciences. Our benchmark is based on the principles of causal graph discovery. It challenges models to uncover hidden structures and make optimal decisions, which includes generating valid justifications. By engaging interactively with an oracle, the models iteratively refine their understanding of underlying interactions, the chemistry and social interactions, through strategic interventions. We evaluate state-of-the-art LLMs, including GPT-4, Gemini, Qwen, Claude, and Llama, and observe a significant performance drop as the problem complexity increases, which suggests an important gap between machine and human intelligence that future development of LLMs need to take into consideration.

Multi-Novelty: Improve the Diversity and Novelty of Contents Generated by Large Language Models via inference-time Multi-Views Brainstorming

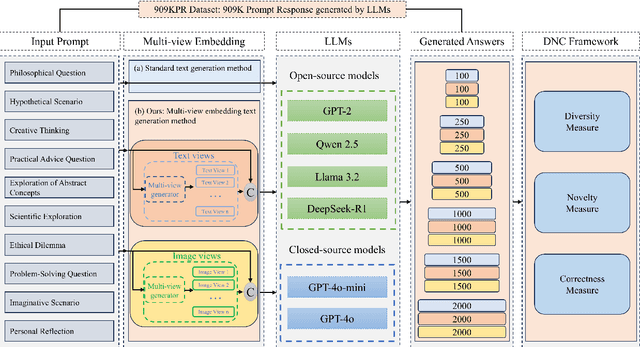
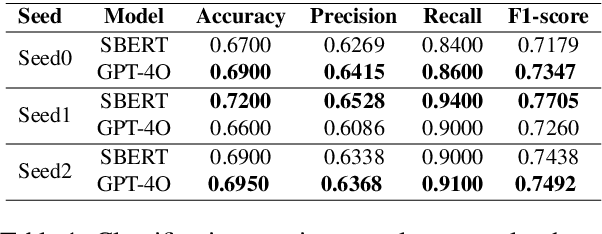
Large Language Models (LLMs) demonstrate remarkable proficiency in generating accurate and fluent text. However, they often struggle with diversity and novelty, leading to repetitive or overly deterministic responses. These limitations stem from constraints in training data, including gaps in specific knowledge domains, outdated information, and an over-reliance on textual sources. Such shortcomings reduce their effectiveness in tasks requiring creativity, multi-perspective reasoning, and exploratory thinking, such as LLM based AI scientist agents and creative artist agents . To address this challenge, we introduce inference-time multi-view brainstorming method, a novel approach that enriches input prompts with diverse perspectives derived from both textual and visual sources, which we refere to as "Multi-Novelty". By incorporating additional contextual information as diverse starting point for chain of thoughts, this method enhances the variety and creativity of generated outputs. Importantly, our approach is model-agnostic, requiring no architectural modifications and being compatible with both open-source and proprietary LLMs.

Continuous Depth Recurrent Neural Differential Equations

Recurrent neural networks (RNNs) have brought a lot of advancements in sequence labeling tasks and sequence data. However, their effectiveness is limited when the observations in the sequence are irregularly sampled, where the observations arrive at irregular time intervals. To address this, continuous time variants of the RNNs were introduced based on neural ordinary differential equations (NODE). They learn a better representation of the data using the continuous transformation of hidden states over time, taking into account the time interval between the observations. However, they are still limited in their capability as they use the discrete transformations and a fixed discrete number of layers (depth) over an input in the sequence to produce the output observation. We intend to address this limitation by proposing RNNs based on differential equations which model continuous transformations over both depth and time to predict an output for a given input in the sequence. Specifically, we propose continuous depth recurrent neural differential equations (CDR-NDE) which generalizes RNN models by continuously evolving the hidden states in both the temporal and depth dimensions. CDR-NDE considers two separate differential equations over each of these dimensions and models the evolution in the temporal and depth directions alternatively. We also propose the CDR-NDE-heat model based on partial differential equations which treats the computation of hidden states as solving a heat equation over time. We demonstrate the effectiveness of the proposed models by comparing against the state-of-the-art RNN models on real world sequence labeling problems and data.

Bi-Directional Recurrent Neural Ordinary Differential Equations for Social Media Text Classification

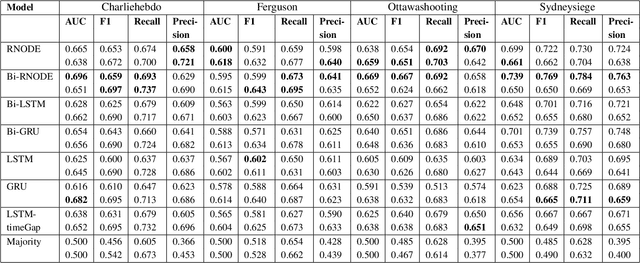
Classification of posts in social media such as Twitter is difficult due to the noisy and short nature of texts. Sequence classification models based on recurrent neural networks (RNN) are popular for classifying posts that are sequential in nature. RNNs assume the hidden representation dynamics to evolve in a discrete manner and do not consider the exact time of the posting. In this work, we propose to use recurrent neural ordinary differential equations (RNODE) for social media post classification which consider the time of posting and allow the computation of hidden representation to evolve in a time-sensitive continuous manner. In addition, we propose a novel model, Bi-directional RNODE (Bi-RNODE), which can consider the information flow in both the forward and backward directions of posting times to predict the post label. Our experiments demonstrate that RNODE and Bi-RNODE are effective for the problem of stance classification of rumours in social media.

Latent Time Neural Ordinary Differential Equations

Neural ordinary differential equations (NODE) have been proposed as a continuous depth generalization to popular deep learning models such as Residual networks (ResNets). They provide parameter efficiency and automate the model selection process in deep learning models to some extent. However, they lack the much-required uncertainty modelling and robustness capabilities which are crucial for their use in several real-world applications such as autonomous driving and healthcare. We propose a novel and unique approach to model uncertainty in NODE by considering a distribution over the end-time $T$ of the ODE solver. The proposed approach, latent time NODE (LT-NODE), treats $T$ as a latent variable and apply Bayesian learning to obtain a posterior distribution over $T$ from the data. In particular, we use variational inference to learn an approximate posterior and the model parameters. Prediction is done by considering the NODE representations from different samples of the posterior and can be done efficiently using a single forward pass. As $T$ implicitly defines the depth of a NODE, posterior distribution over $T$ would also help in model selection in NODE. We also propose, adaptive latent time NODE (ALT-NODE), which allow each data point to have a distinct posterior distribution over end-times. ALT-NODE uses amortized variational inference to learn an approximate posterior using inference networks. We demonstrate the effectiveness of the proposed approaches in modelling uncertainty and robustness through experiments on synthetic and several real-world image classification data.

Improving Robustness and Uncertainty Modelling in Neural Ordinary Differential Equations

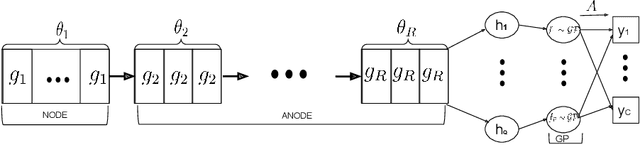
Neural ordinary differential equations (NODE) have been proposed as a continuous depth generalization to popular deep learning models such as Residual networks (ResNets). They provide parameter efficiency and automate the model selection process in deep learning models to some extent. However, they lack the much-required uncertainty modelling and robustness capabilities which are crucial for their use in several real-world applications such as autonomous driving and healthcare. We propose a novel and unique approach to model uncertainty in NODE by considering a distribution over the end-time $T$ of the ODE solver. The proposed approach, latent time NODE (LT-NODE), treats $T$ as a latent variable and apply Bayesian learning to obtain a posterior distribution over $T$ from the data. In particular, we use variational inference to learn an approximate posterior and the model parameters. Prediction is done by considering the NODE representations from different samples of the posterior and can be done efficiently using a single forward pass. As $T$ implicitly defines the depth of a NODE, posterior distribution over $T$ would also help in model selection in NODE. We also propose, adaptive latent time NODE (ALT-NODE), which allow each data point to have a distinct posterior distribution over end-times. ALT-NODE uses amortized variational inference to learn an approximate posterior using inference networks. We demonstrate the effectiveness of the proposed approaches in modelling uncertainty and robustness through experiments on synthetic and several real-world image classification data.

Delay Differential Neural Networks

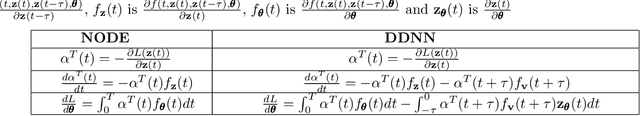
Neural ordinary differential equations (NODEs) treat computation of intermediate feature vectors as trajectories of ordinary differential equation parameterized by a neural network. In this paper, we propose a novel model, delay differential neural networks (DDNN), inspired by delay differential equations (DDEs). The proposed model considers the derivative of the hidden feature vector as a function of the current feature vector and past feature vectors (history). The function is modelled as a neural network and consequently, it leads to continuous depth alternatives to many recent ResNet variants. We propose two different DDNN architectures, depending on the way current and past feature vectors are considered. For training DDNNs, we provide a memory-efficient adjoint method for computing gradients and back-propagate through the network. DDNN improves the data efficiency of NODE by further reducing the number of parameters without affecting the generalization performance. Experiments conducted on synthetic and real-world image classification datasets such as Cifar10 and Cifar100 show the effectiveness of the proposed models.