Delay Differential Neural Networks
Paper and Code
Dec 12, 2020
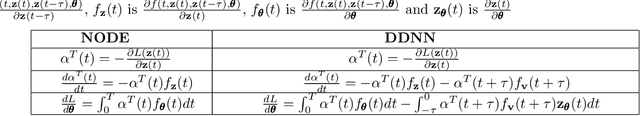


Neural ordinary differential equations (NODEs) treat computation of intermediate feature vectors as trajectories of ordinary differential equation parameterized by a neural network. In this paper, we propose a novel model, delay differential neural networks (DDNN), inspired by delay differential equations (DDEs). The proposed model considers the derivative of the hidden feature vector as a function of the current feature vector and past feature vectors (history). The function is modelled as a neural network and consequently, it leads to continuous depth alternatives to many recent ResNet variants. We propose two different DDNN architectures, depending on the way current and past feature vectors are considered. For training DDNNs, we provide a memory-efficient adjoint method for computing gradients and back-propagate through the network. DDNN improves the data efficiency of NODE by further reducing the number of parameters without affecting the generalization performance. Experiments conducted on synthetic and real-world image classification datasets such as Cifar10 and Cifar100 show the effectiveness of the proposed models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge