Impact Measures for Gradual Argumentation Semantics

Argumentation is a formalism allowing to reason with contradictory information by modeling arguments and their interactions. There are now an increasing number of gradual semantics and impact measures that have emerged to facilitate the interpretation of their outcomes. An impact measure assesses, for each argument, the impact of other arguments on its score. In this paper, we refine an existing impact measure from Delobelle and Villata and introduce a new impact measure rooted in Shapley values. We introduce several principles to evaluate those two impact measures w.r.t. some well-known gradual semantics. This comprehensive analysis provides deeper insights into their functionality and desirability.

The Inverse Problem for Argumentation Gradual Semantics

Gradual semantics with abstract argumentation provide each argument with a score reflecting its acceptability, i.e. how "much" it is attacked by other arguments. Many different gradual semantics have been proposed in the literature, each following different principles and producing different argument rankings. A sub-class of such semantics, the so-called weighted semantics, takes, in addition to the graph structure, an initial set of weights over the arguments as input, with these weights affecting the resultant argument ranking. In this work, we consider the inverse problem over such weighted semantics. That is, given an argumentation framework and a desired argument ranking, we ask whether there exist initial weights such that a particular semantics produces the given ranking. The contribution of this paper are: (1) an algorithm to answer this problem, (2) a characterisation of the properties that a gradual semantics must satisfy for the algorithm to operate, and (3) an empirical evaluation of the proposed algorithm.

Dung's semantics satisfy attack removal monotonicity

We show that preferred, stable, complete, and grounded semantics satisfy attack removal monotonicity. This means that if an attack from b to a is removed, the status of a cannot worsen, e.g. if a was skeptically accepted, it cannot become rejected.

Representing Pure Nash Equilibria in Argumentation

In this paper we describe an argumentation-based representation of normal form games, and demonstrate how argumentation can be used to compute pure strategy Nash equilibria. Our approach builds on Modgil's Extended Argumentation Frameworks. We demonstrate its correctness, prove several theoretical properties it satisfies, and outline how it can be used to explain why certain strategies are Nash equilibria to a non-expert human user.

A note on the uniqueness of models in social abstract argumentation

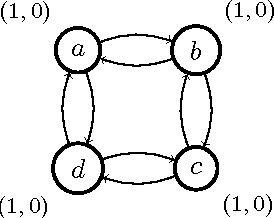
Social abstract argumentation is a principled way to assign values to conflicting (weighted) arguments. In this note we discuss the important property of the uniqueness of the model.

A partial taxonomy of judgment aggregation rules, and their properties

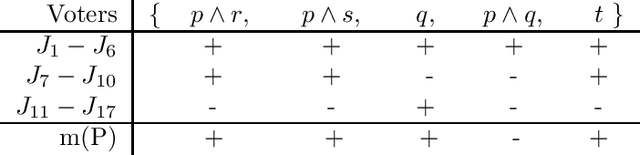
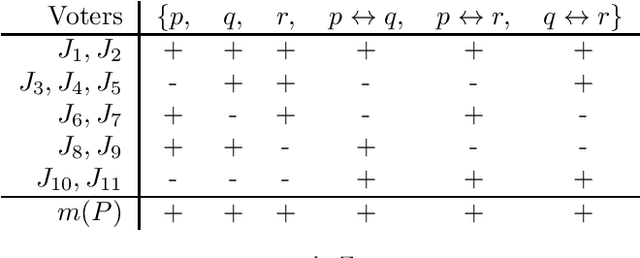
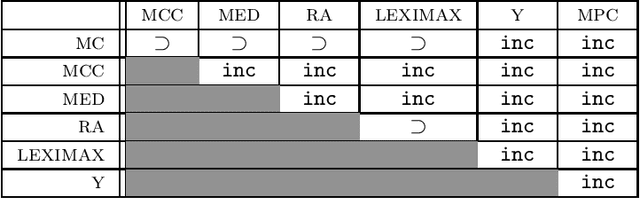
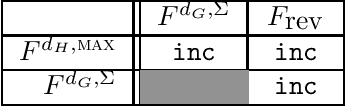
The literature on judgment aggregation is moving from studying impossibility results regarding aggregation rules towards studying specific judgment aggregation rules. Here we give a structured list of most rules that have been proposed and studied recently in the literature, together with various properties of such rules. We first focus on the majority-preservation property, which generalizes Condorcet-consistency, and identify which of the rules satisfy it. We study the inclusion relationships that hold between the rules. Finally, we consider two forms of unanimity, monotonicity, homogeneity, and reinforcement, and we identify which of the rules satisfy these properties.

Agenda Separability in Judgment Aggregation

One of the better studied properties for operators in judgment aggregation is independence, which essentially dictates that the collective judgment on one issue should not depend on the individual judgments given on some other issue(s) in the same agenda. Independence, although considered a desirable property, is too strong, because together with mild additional conditions it implies dictatorship. We propose here a weakening of independence, named agenda separability: a judgment aggregation rule satisfies it if, whenever the agenda is composed of several independent sub-agendas, the resulting collective judgment sets can be computed separately for each sub-agenda and then put together. We show that this property is discriminant, in the sense that among judgment aggregation rules so far studied in the literature, some satisfy it and some do not. We briefly discuss the implications of agenda separability on the computation of judgment aggregation rules.

Identifying the Class of Maxi-Consistent Operators in Argumentation

Dung's abstract argumentation theory can be seen as a general framework for non-monotonic reasoning. An important question is then: what is the class of logics that can be subsumed as instantiations of this theory? The goal of this paper is to identify and study the large class of logic-based instantiations of Dung's theory which correspond to the maxi-consistent operator, i.e. to the function which returns maximal consistent subsets of an inconsistent knowledge base. In other words, we study the class of instantiations where very extension of the argumentation system corresponds to exactly one maximal consistent subset of the knowledge base. We show that an attack relation belonging to this class must be conflict-dependent, must not be valid, must not be conflict-complete, must not be symmetric etc. Then, we show that some attack relations serve as lower or upper bounds of the class (e.g. if an attack relation contains canonical undercut then it is not a member of this class). By using our results, we show for all existing attack relations whether or not they belong to this class. We also define new attack relations which are members of this class. Finally, we interpret our results and discuss more general questions, like: what is the added value of argumentation in such a setting? We believe that this work is a first step towards achieving our long-term goal, which is to better understand the role of argumentation and, particularly, the expressivity of logic-based instantiations of Dung-style argumentation frameworks.