TD-TOG Dataset: Benchmarking Zero-Shot and One-Shot Task-Oriented Grasping for Object Generalization

Task-oriented grasping (TOG) is an essential preliminary step for robotic task execution, which involves predicting grasps on regions of target objects that facilitate intended tasks. Existing literature reveals there is a limited availability of TOG datasets for training and benchmarking despite large demand, which are often synthetic or have artifacts in mask annotations that hinder model performance. Moreover, TOG solutions often require affordance masks, grasps, and object masks for training, however, existing datasets typically provide only a subset of these annotations. To address these limitations, we introduce the Top-down Task-oriented Grasping (TD-TOG) dataset, designed to train and evaluate TOG solutions. TD-TOG comprises 1,449 real-world RGB-D scenes including 30 object categories and 120 subcategories, with hand-annotated object masks, affordances, and planar rectangular grasps. It also features a test set for a novel challenge that assesses a TOG solution's ability to distinguish between object subcategories. To contribute to the demand for TOG solutions that can adapt and manipulate previously unseen objects without re-training, we propose a novel TOG framework, Binary-TOG. Binary-TOG uses zero-shot for object recognition, and one-shot learning for affordance recognition. Zero-shot learning enables Binary-TOG to identify objects in multi-object scenes through textual prompts, eliminating the need for visual references. In multi-object settings, Binary-TOG achieves an average task-oriented grasp accuracy of 68.9%. Lastly, this paper contributes a comparative analysis between one-shot and zero-shot learning for object generalization in TOG to be used in the development of future TOG solutions.

VIRAL: Vision-grounded Integration for Reward design And Learning

The alignment between humans and machines is a critical challenge in artificial intelligence today. Reinforcement learning, which aims to maximize a reward function, is particularly vulnerable to the risks associated with poorly designed reward functions. Recent advancements has shown that Large Language Models (LLMs) for reward generation can outperform human performance in this context. We introduce VIRAL, a pipeline for generating and refining reward functions through the use of multi-modal LLMs. VIRAL autonomously creates and interactively improves reward functions based on a given environment and a goal prompt or annotated image. The refinement process can incorporate human feedback or be guided by a description generated by a video LLM, which explains the agent's policy in video form. We evaluated VIRAL in five Gymnasium environments, demonstrating that it accelerates the learning of new behaviors while ensuring improved alignment with user intent. The source-code and demo video are available at: https://github.com/VIRAL-UCBL1/VIRAL and https://youtu.be/t4_BXugBm9Q.

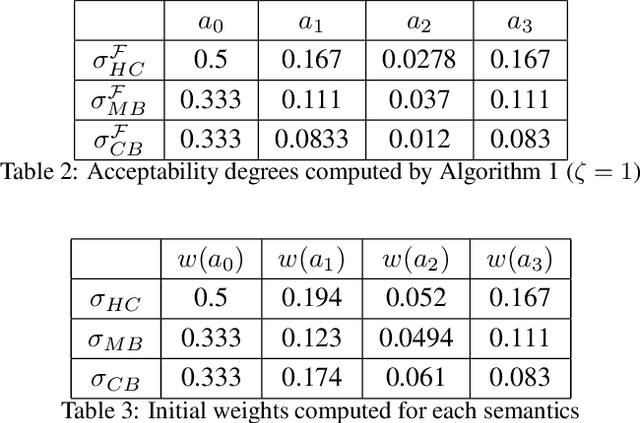
Eliciting Rational Initial Weights in Gradual Argumentation

Many semantics for weighted argumentation frameworks assume that each argument is associated with an initial weight. However, eliciting these initial weights poses challenges: (1) accurately providing a specific numerical value is often difficult, and (2) individuals frequently confuse initial weights with acceptability degrees in the presence of other arguments. To address these issues, we propose an elicitation pipeline that allows one to specify acceptability degree intervals for each argument. By employing gradual semantics, we can refine these intervals when they are rational, restore rationality when they are not, and ultimately identify possible initial weights for each argument.

Leveraging Graph Structures and Large Language Models for End-to-End Synthetic Task-Oriented Dialogues

Training task-oriented dialogue systems is both costly and time-consuming, due to the need for high-quality datasets encompassing diverse intents. Traditional methods depend on extensive human annotation, while recent advancements leverage large language models (LLMs) to generate synthetic data. However, these approaches often require custom prompts or code, limiting accessibility for non-technical users. We introduce GraphTOD, an end-to-end framework that simplifies the generation of task-oriented dialogues. Users can create dialogues by specifying transition graphs in JSON format. Our evaluation demonstrates that GraphTOD generates high-quality dialogues across various domains, significantly lowering the cost and complexity of dataset creation.

Impact Measures for Gradual Argumentation Semantics

Argumentation is a formalism allowing to reason with contradictory information by modeling arguments and their interactions. There are now an increasing number of gradual semantics and impact measures that have emerged to facilitate the interpretation of their outcomes. An impact measure assesses, for each argument, the impact of other arguments on its score. In this paper, we refine an existing impact measure from Delobelle and Villata and introduce a new impact measure rooted in Shapley values. We introduce several principles to evaluate those two impact measures w.r.t. some well-known gradual semantics. This comprehensive analysis provides deeper insights into their functionality and desirability.

Abstract Weighted Based Gradual Semantics in Argumentation Theory

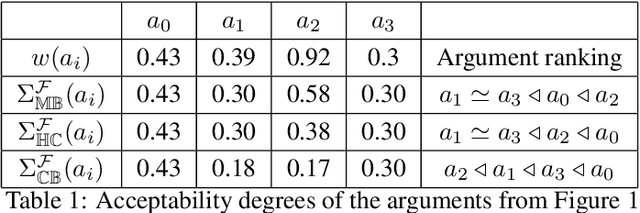
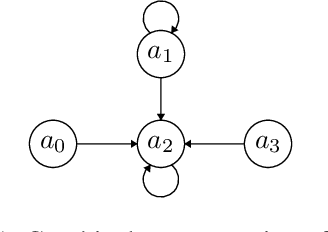
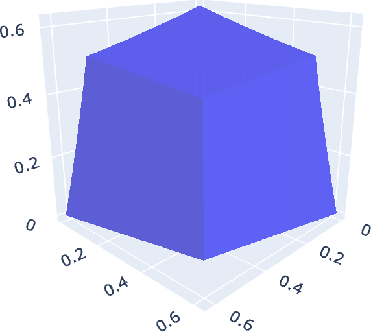
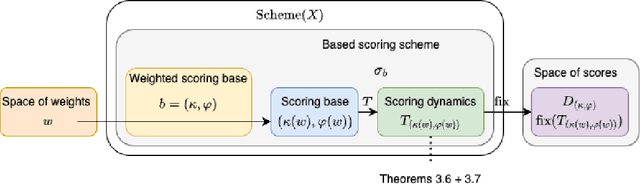
Weighted gradual semantics provide an acceptability degree to each argument representing the strength of the argument, computed based on factors including background evidence for the argument, and taking into account interactions between this argument and others. We introduce four important problems linking gradual semantics and acceptability degrees. First, we reexamine the inverse problem, seeking to identify the argument weights of the argumentation framework which lead to a specific final acceptability degree. Second, we ask whether the function mapping between argument weights and acceptability degrees is injective or a homeomorphism onto its image. Third, we ask whether argument weights can be found when preferences, rather than acceptability degrees for arguments are considered. Fourth, we consider the topology of the space of valid acceptability degrees, asking whether gaps exist in this space. While different gradual semantics have been proposed in the literature, in this paper, we identify a large family of weighted gradual semantics, called abstract weighted based gradual semantics. These generalise many of the existing semantics while maintaining desirable properties such as convergence to a unique fixed point. We also show that a sub-family of the weighted gradual semantics, called abstract weighted (Lp,lambda,mu,A)-based gradual semantics and which include well-known semantics, solve all four of the aforementioned problems.

Inferring Attack Relations for Gradual Semantics

A gradual semantics takes a weighted argumentation framework as input and outputs a final acceptability degree for each argument, with different semantics performing the computation in different manners. In this work, we consider the problem of attack inference. That is, given a gradual semantics, a set of arguments with associated initial weights, and the final desirable acceptability degrees associated with each argument, we seek to determine whether there is a set of attacks on those arguments such that we can obtain these acceptability degrees. The main contribution of our work is to demonstrate that the associated decision problem, i.e., whether a set of attacks can exist which allows the final acceptability degrees to occur for given initial weights, is NP-complete for the weighted h-categoriser and cardinality-based semantics, and is polynomial for the weighted max-based semantics, even for the complete version of the problem (where all initial weights and final acceptability degrees are known). We then briefly discuss how this decision problem can be modified to find the attacks themselves and conclude by examining the partial problem where not all initial weights or final acceptability degrees may be known.

Utility Functions for Human/Robot Interaction

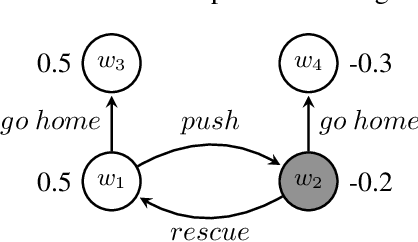
In this paper, we place ourselves in the context of human robot interaction and address the problem of cognitive robot modelling. More precisely we are investigating properties of a utility-based model that will govern a robot's actions. The novelty of this approach lies in embedding the responsibility of the robot over the state of affairs into the utility model via a utility aggregation function. We describe desiderata for such a function and consider related properties.

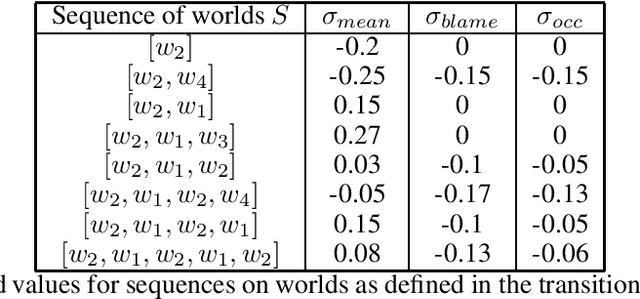
Analytical Solutions for the Inverse Problem within Gradual Semantics

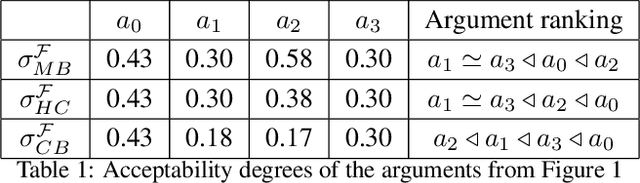
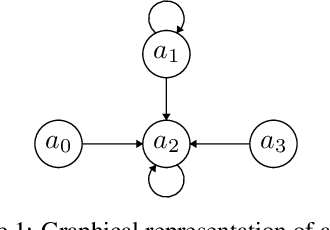
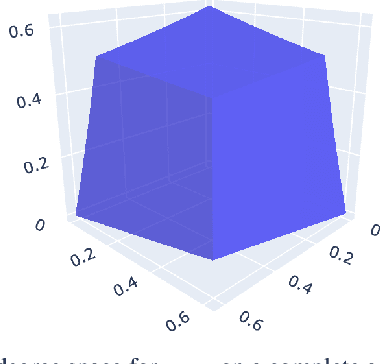
Gradual semantics within abstract argumentation associate a numeric score with every argument in a system, which represents the level of acceptability of this argument, and from which a preference ordering over arguments can be derived. While some semantics operate over standard argumentation frameworks, many utilise a weighted framework, where a numeric initial weight is associated with each argument. Recent work has examined the inverse problem within gradual semantics. Rather than determining a preference ordering given an argumentation framework and a semantics, the inverse problem takes an argumentation framework, a gradual semantics, and a preference ordering as inputs, and identifies what weights are needed to over arguments in the framework to obtain the desired preference ordering. Existing work has attacked the inverse problem numerically, using a root finding algorithm (the bisection method) to identify appropriate initial weights. In this paper we demonstrate that for a class of gradual semantics, an analytical approach can be used to solve the inverse problem. Unlike the current state-of-the-art, such an analytic approach can rapidly find a solution, and is guaranteed to do so. In obtaining this result, we are able to prove several important properties which previous work had posed as conjectures.

The Inverse Problem for Argumentation Gradual Semantics

Gradual semantics with abstract argumentation provide each argument with a score reflecting its acceptability, i.e. how "much" it is attacked by other arguments. Many different gradual semantics have been proposed in the literature, each following different principles and producing different argument rankings. A sub-class of such semantics, the so-called weighted semantics, takes, in addition to the graph structure, an initial set of weights over the arguments as input, with these weights affecting the resultant argument ranking. In this work, we consider the inverse problem over such weighted semantics. That is, given an argumentation framework and a desired argument ranking, we ask whether there exist initial weights such that a particular semantics produces the given ranking. The contribution of this paper are: (1) an algorithm to answer this problem, (2) a characterisation of the properties that a gradual semantics must satisfy for the algorithm to operate, and (3) an empirical evaluation of the proposed algorithm.