Abstract Weighted Based Gradual Semantics in Argumentation Theory

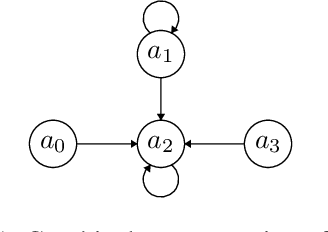
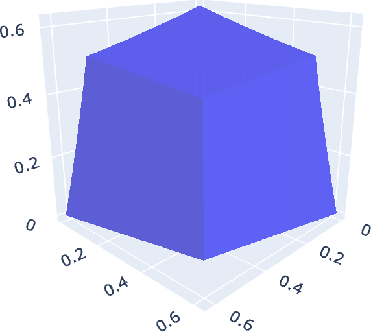
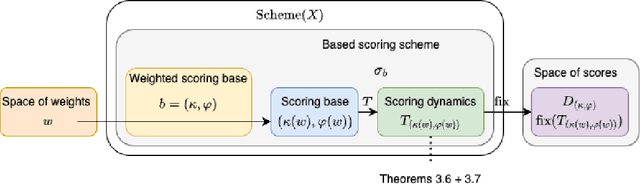
Weighted gradual semantics provide an acceptability degree to each argument representing the strength of the argument, computed based on factors including background evidence for the argument, and taking into account interactions between this argument and others. We introduce four important problems linking gradual semantics and acceptability degrees. First, we reexamine the inverse problem, seeking to identify the argument weights of the argumentation framework which lead to a specific final acceptability degree. Second, we ask whether the function mapping between argument weights and acceptability degrees is injective or a homeomorphism onto its image. Third, we ask whether argument weights can be found when preferences, rather than acceptability degrees for arguments are considered. Fourth, we consider the topology of the space of valid acceptability degrees, asking whether gaps exist in this space. While different gradual semantics have been proposed in the literature, in this paper, we identify a large family of weighted gradual semantics, called abstract weighted based gradual semantics. These generalise many of the existing semantics while maintaining desirable properties such as convergence to a unique fixed point. We also show that a sub-family of the weighted gradual semantics, called abstract weighted (Lp,lambda,mu,A)-based gradual semantics and which include well-known semantics, solve all four of the aforementioned problems.