Analytical Solutions for the Inverse Problem within Gradual Semantics

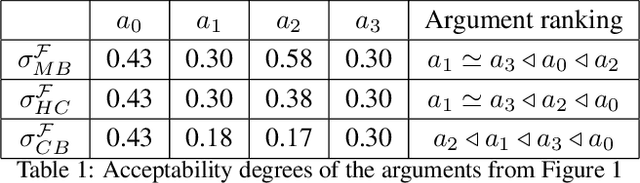
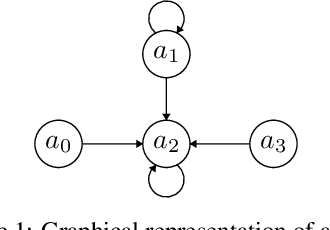
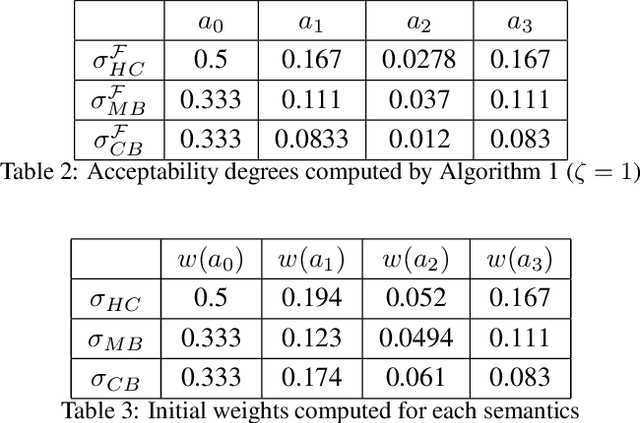
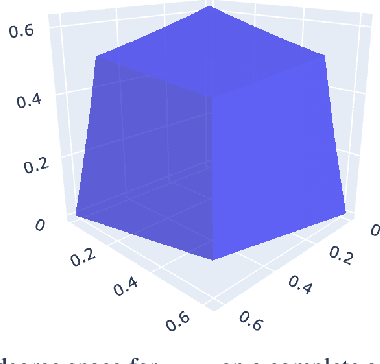
Gradual semantics within abstract argumentation associate a numeric score with every argument in a system, which represents the level of acceptability of this argument, and from which a preference ordering over arguments can be derived. While some semantics operate over standard argumentation frameworks, many utilise a weighted framework, where a numeric initial weight is associated with each argument. Recent work has examined the inverse problem within gradual semantics. Rather than determining a preference ordering given an argumentation framework and a semantics, the inverse problem takes an argumentation framework, a gradual semantics, and a preference ordering as inputs, and identifies what weights are needed to over arguments in the framework to obtain the desired preference ordering. Existing work has attacked the inverse problem numerically, using a root finding algorithm (the bisection method) to identify appropriate initial weights. In this paper we demonstrate that for a class of gradual semantics, an analytical approach can be used to solve the inverse problem. Unlike the current state-of-the-art, such an analytic approach can rapidly find a solution, and is guaranteed to do so. In obtaining this result, we are able to prove several important properties which previous work had posed as conjectures.

Delegating via Quitting Games

Delegation allows an agent to request that another agent completes a task. In many situations the task may be delegated onwards, and this process can repeat until it is eventually, successfully or unsuccessfully, performed. We consider policies to guide an agent in choosing who to delegate to when such recursive interactions are possible. These policies, based on quitting games and multi-armed bandits, were empirically tested for effectiveness. Our results indicate that the quitting game based policies outperform those which do not explicitly account for the recursive nature of delegation.