Sobhan Naderi Parizi
Generalized Majorization-Minimization
Jul 28, 2016
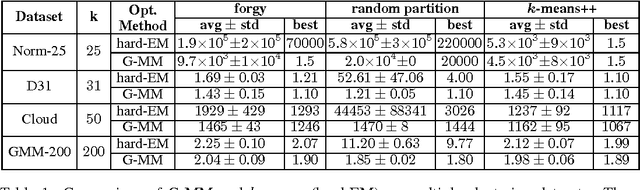
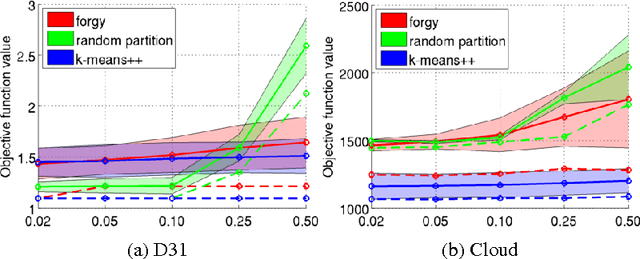

Abstract:Non-convex optimization is ubiquitous in machine learning. The Majorization-Minimization (MM) procedure systematically optimizes non-convex functions through an iterative construction and optimization of upper bounds on the objective function. The bound at each iteration is required to \emph{touch} the objective function at the optimizer of the previous bound. We show that this touching constraint is unnecessary and overly restrictive. We generalize MM by relaxing this constraint, and propose a new framework for designing optimization algorithms, named Generalized Majorization-Minimization (G-MM). Compared to MM, G-MM is much more flexible. For instance, it can incorporate application-specific biases into the optimization procedure without changing the objective function. We derive G-MM algorithms for several latent variable models and show that they consistently outperform their MM counterparts in optimizing non-convex objectives. In particular, G-MM algorithms appear to be less sensitive to initialization.
Spotlight the Negatives: A Generalized Discriminative Latent Model
Jul 08, 2015


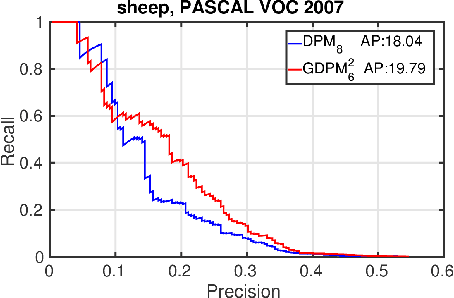
Abstract:Discriminative latent variable models (LVM) are frequently applied to various visual recognition tasks. In these systems the latent (hidden) variables provide a formalism for modeling structured variation of visual features. Conventionally, latent variables are de- fined on the variation of the foreground (positive) class. In this work we augment LVMs to include negative latent variables corresponding to the background class. We formalize the scoring function of such a generalized LVM (GLVM). Then we discuss a framework for learning a model based on the GLVM scoring function. We theoretically showcase how some of the current visual recognition methods can benefit from this generalization. Finally, we experiment on a generalized form of Deformable Part Models with negative latent variables and show significant improvements on two different detection tasks.
Automatic Discovery and Optimization of Parts for Image Classification
Apr 11, 2015

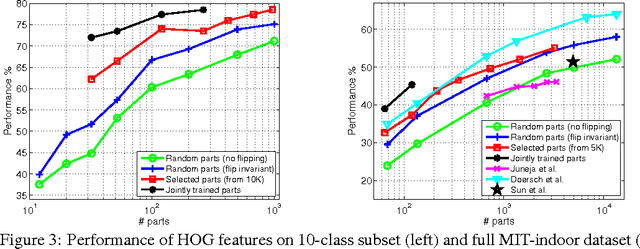
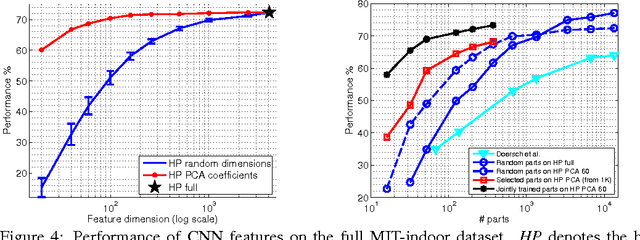
Abstract:Part-based representations have been shown to be very useful for image classification. Learning part-based models is often viewed as a two-stage problem. First, a collection of informative parts is discovered, using heuristics that promote part distinctiveness and diversity, and then classifiers are trained on the vector of part responses. In this paper we unify the two stages and learn the image classifiers and a set of shared parts jointly. We generate an initial pool of parts by randomly sampling part candidates and selecting a good subset using L1/L2 regularization. All steps are driven "directly" by the same objective namely the classification loss on a training set. This lets us do away with engineered heuristics. We also introduce the notion of "negative parts", intended as parts that are negatively correlated with one or more classes. Negative parts are complementary to the parts discovered by other methods, which look only for positive correlations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge