Generalized Majorization-Minimization

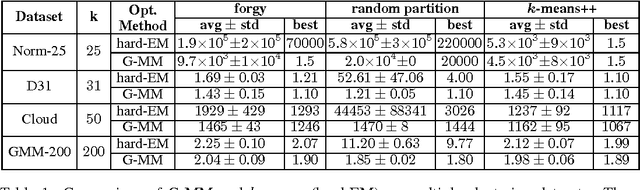
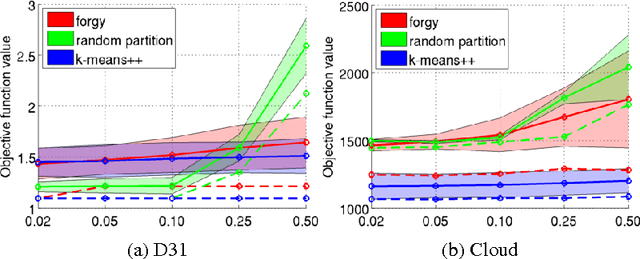
Non-convex optimization is ubiquitous in machine learning. The Majorization-Minimization (MM) procedure systematically optimizes non-convex functions through an iterative construction and optimization of upper bounds on the objective function. The bound at each iteration is required to \emph{touch} the objective function at the optimizer of the previous bound. We show that this touching constraint is unnecessary and overly restrictive. We generalize MM by relaxing this constraint, and propose a new framework for designing optimization algorithms, named Generalized Majorization-Minimization (G-MM). Compared to MM, G-MM is much more flexible. For instance, it can incorporate application-specific biases into the optimization procedure without changing the objective function. We derive G-MM algorithms for several latent variable models and show that they consistently outperform their MM counterparts in optimizing non-convex objectives. In particular, G-MM algorithms appear to be less sensitive to initialization.