Deconvolution with a Box

Deconvolution with a box (square wave) is a key operation for super-resolution with pixel-shift cameras. In general convolution with a box is not invertible. However, we can obtain perfect reconstructions of sparse signals using convex optimization. We give a direct proof that improves on the reconstruction bound that follows from previous results. We also show our bound is tight and matches an information theoretic limit.

Convex Combination Belief Propagation Algorithms

We introduce new message passing algorithms for inference with graphical models. The standard min-sum and sum-product belief propagation algorithms are guaranteed to converge when the graph is tree-structured, but may not converge and can be sensitive to the initialization when the graph contains cycles. This paper describes modifications to the standard belief propagation algorithms that are guaranteed to converge to a unique solution regardless of the topology of the graph.

Direct Estimation of Appearance Models for Segmentation

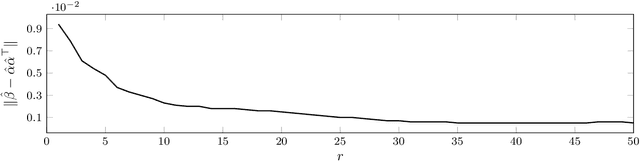
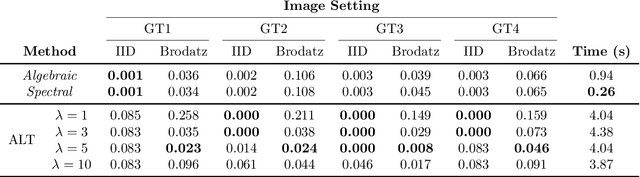
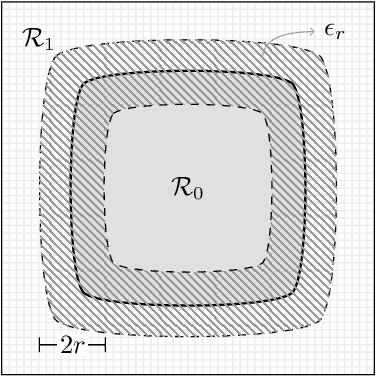
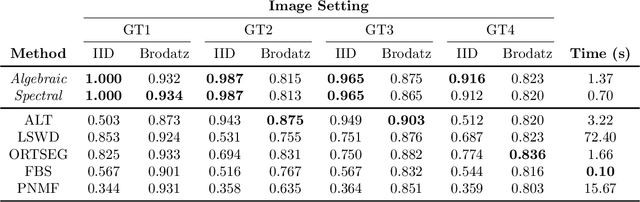
Image segmentation algorithms often depend on appearance models that characterize the distribution of pixel values in different image regions. We describe a novel approach for estimating appearance models directly from an image, without explicit consideration of the pixels that make up each region. Our approach is based on algebraic expressions that relate local image statistics to the appearance models of spatially coherent regions. We describe two algorithms that can use the aforementioned algebraic expressions for estimating appearance models. The first algorithm is based on solving a system of linear and quadratic equations. The second algorithm is a spectral method based on an eigenvector computation. We present experimental results that demonstrate the proposed methods work well in practice and lead to effective image segmentation algorithms.

Clustering with Iterated Linear Optimization

We introduce a novel method for clustering using a semidefinite programming (SDP) relaxation of the Max k-Cut problem. The approach is based on a new methodology for rounding the solution of an SDP using iterated linear optimization. We show the vertices of the Max k-Cut SDP relaxation correspond to partitions of the data into at most k sets. We also show the vertices are attractive fixed points of iterated linear optimization. We interpret the process of fixed point iteration with linear optimization as repeated relaxations of the closest vertex problem. Our experiments show that using fixed point iteration for rounding the Max k-Cut SDP relaxation leads to significantly better results when compared to randomized rounding.

Generalized Majorization-Minimization

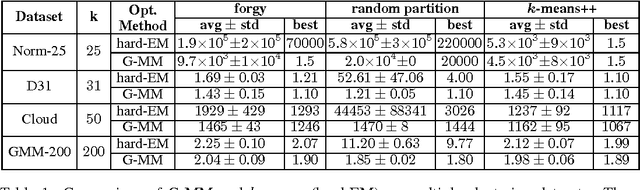
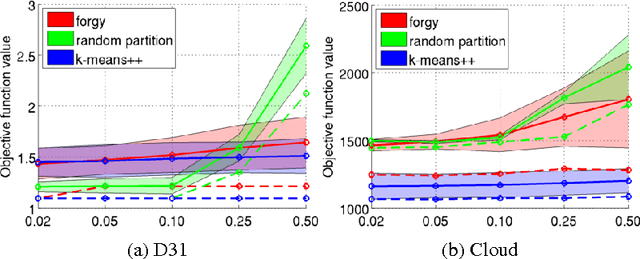
Non-convex optimization is ubiquitous in machine learning. The Majorization-Minimization (MM) procedure systematically optimizes non-convex functions through an iterative construction and optimization of upper bounds on the objective function. The bound at each iteration is required to \emph{touch} the objective function at the optimizer of the previous bound. We show that this touching constraint is unnecessary and overly restrictive. We generalize MM by relaxing this constraint, and propose a new framework for designing optimization algorithms, named Generalized Majorization-Minimization (G-MM). Compared to MM, G-MM is much more flexible. For instance, it can incorporate application-specific biases into the optimization procedure without changing the objective function. We derive G-MM algorithms for several latent variable models and show that they consistently outperform their MM counterparts in optimizing non-convex objectives. In particular, G-MM algorithms appear to be less sensitive to initialization.

Automatic Discovery and Optimization of Parts for Image Classification

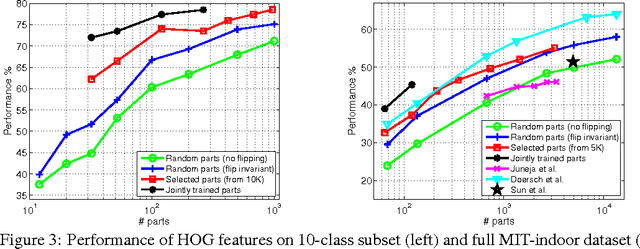
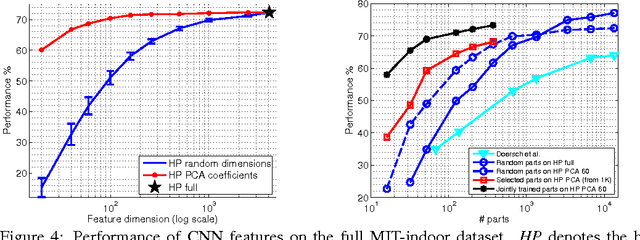
Part-based representations have been shown to be very useful for image classification. Learning part-based models is often viewed as a two-stage problem. First, a collection of informative parts is discovered, using heuristics that promote part distinctiveness and diversity, and then classifiers are trained on the vector of part responses. In this paper we unify the two stages and learn the image classifiers and a set of shared parts jointly. We generate an initial pool of parts by randomly sampling part candidates and selecting a good subset using L1/L2 regularization. All steps are driven "directly" by the same objective namely the classification loss on a training set. This lets us do away with engineered heuristics. We also introduce the notion of "negative parts", intended as parts that are negatively correlated with one or more classes. Negative parts are complementary to the parts discovered by other methods, which look only for positive correlations.