Direct Estimation of Appearance Models for Segmentation

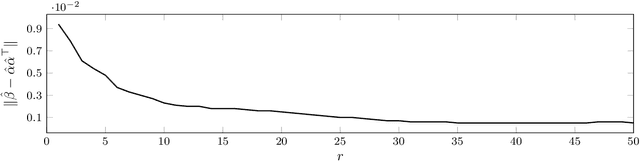
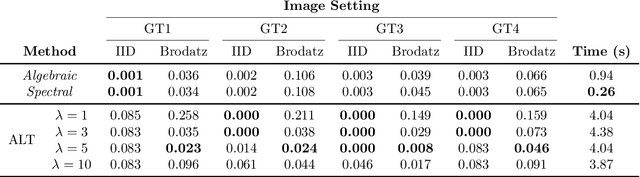
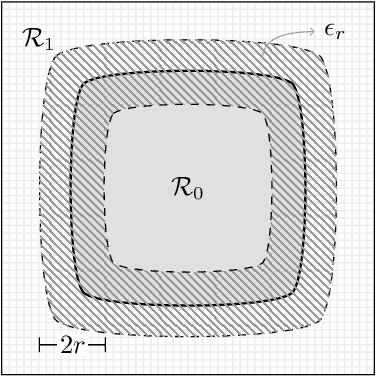
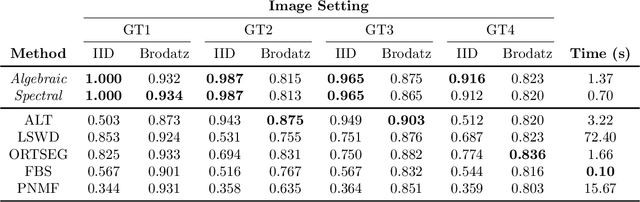
Image segmentation algorithms often depend on appearance models that characterize the distribution of pixel values in different image regions. We describe a novel approach for estimating appearance models directly from an image, without explicit consideration of the pixels that make up each region. Our approach is based on algebraic expressions that relate local image statistics to the appearance models of spatially coherent regions. We describe two algorithms that can use the aforementioned algebraic expressions for estimating appearance models. The first algorithm is based on solving a system of linear and quadratic equations. The second algorithm is a spectral method based on an eigenvector computation. We present experimental results that demonstrate the proposed methods work well in practice and lead to effective image segmentation algorithms.

Spectral Image Segmentation with Global Appearance Modeling

We introduce a new spectral method for image segmentation that incorporates long range relationships for global appearance modeling. The approach combines two different graphs, one is a sparse graph that captures spatial relationships between nearby pixels and another is a dense graph that captures pairwise similarity between all pairs of pixels. We extend the spectral method for Normalized Cuts to this setting by combining the transition matrices of Markov chains associated with each graph. We also derive an efficient method that uses importance sampling for sparsifying the dense graph of appearance relationships. This leads to a practical algorithm for segmenting high-resolution images. The resulting method can segment challenging images without any filtering or pre-processing.