DAG Learning from Zero-Inflated Count Data Using Continuous Optimization

We address network structure learning from zero-inflated count data by casting each node as a zero-inflated generalized linear model and optimizing a smooth, score-based objective under a directed acyclic graph constraint. Our Zero-Inflated Continuous Optimization (ZICO) approach uses node-wise likelihoods with canonical links and enforces acyclicity through a differentiable surrogate constraint combined with sparsity regularization. ZICO achieves superior performance with faster runtimes on simulated data. It also performs comparably to or better than common algorithms for reverse engineering gene regulatory networks. ZICO is fully vectorized and mini-batched, enabling learning on larger variable sets with practical runtimes in a wide range of domains.

Practical Causal Evaluation Metrics for Biological Networks

Estimating causal networks from biological data is a critical step in systems biology. When evaluating the inferred network, assessing the networks based on their intervention effects is particularly important for downstream probabilistic reasoning and the identification of potential drug targets. In the context of gene regulatory network inference, biological databases are often used as reference sources. These databases typically describe relationships in a qualitative rather than quantitative manner. However, few evaluation metrics have been developed that take this qualitative nature into account. To address this, we developed a metric, the sign-augmented Structural Intervention Distance (sSID), and a weighted sSID that incorporates the net effects of the intervention. Through simulations and analyses of real transcriptomic datasets, we found that our proposed metrics could identify a different algorithm as optimal compared to conventional metrics, and the network selected by sSID had a superior performance in the classification task of clinical covariates using transcriptomic data. This suggests that sSID can distinguish networks that are structurally correct but functionally incorrect, highlighting its potential as a more biologically meaningful and practical evaluation metric.

Multi-task learning via robust regularized clustering with non-convex group penalties

Multi-task learning (MTL) aims to improve estimation and prediction performance by sharing common information among related tasks. One natural assumption in MTL is that tasks are classified into clusters based on their characteristics. However, existing MTL methods based on this assumption often ignore outlier tasks that have large task-specific components or no relation to other tasks. To address this issue, we propose a novel MTL method called Multi-Task Learning via Robust Regularized Clustering (MTLRRC). MTLRRC incorporates robust regularization terms inspired by robust convex clustering, which is further extended to handle non-convex and group-sparse penalties. The extension allows MTLRRC to simultaneously perform robust task clustering and outlier task detection. The connection between the extended robust clustering and the multivariate M-estimator is also established. This provides an interpretation of the robustness of MTLRRC against outlier tasks. An efficient algorithm based on a modified alternating direction method of multipliers is developed for the estimation of the parameters. The effectiveness of MTLRRC is demonstrated through simulation studies and application to real data.

Multi-Task Learning Regression via Convex Clustering

Multi-task learning (MTL) is a methodology that aims to improve the general performance of estimation and prediction by sharing common information among related tasks. In the MTL, there are several assumptions for the relationships and methods to incorporate them. One of the natural assumptions in the practical situation is that tasks are classified into some clusters with their characteristics. For this assumption, the group fused regularization approach performs clustering of the tasks by shrinking the difference among tasks. This enables us to transfer common information within the same cluster. However, this approach also transfers the information between different clusters, which worsens the estimation and prediction. To overcome this problem, we propose an MTL method with a centroid parameter representing a cluster center of the task. Because this model separates parameters into the parameters for regression and the parameters for clustering, we can improve estimation and prediction accuracy for regression coefficient vectors. We show the effectiveness of the proposed method through Monte Carlo simulations and applications to real data.

Multivariate regression modeling in integrative analysis via sparse regularization

The multivariate regression model basically offers the analysis of a single dataset with multiple responses. However, such a single-dataset analysis often leads to unsatisfactory results. Integrative analysis is an effective method to pool useful information from multiple independent datasets and provides better performance than single-dataset analysis. In this study, we propose a multivariate regression modeling in integrative analysis. The integration is achieved by sparse estimation that performs variable and group selection. Based on the idea of alternating direction method of multipliers, we develop its computational algorithm that enjoys the convergence property. The performance of the proposed method is demonstrated through Monte Carlo simulation and analyzing wastewater treatment data with microbe measurements.

A Bayesian approach to multi-task learning with network lasso

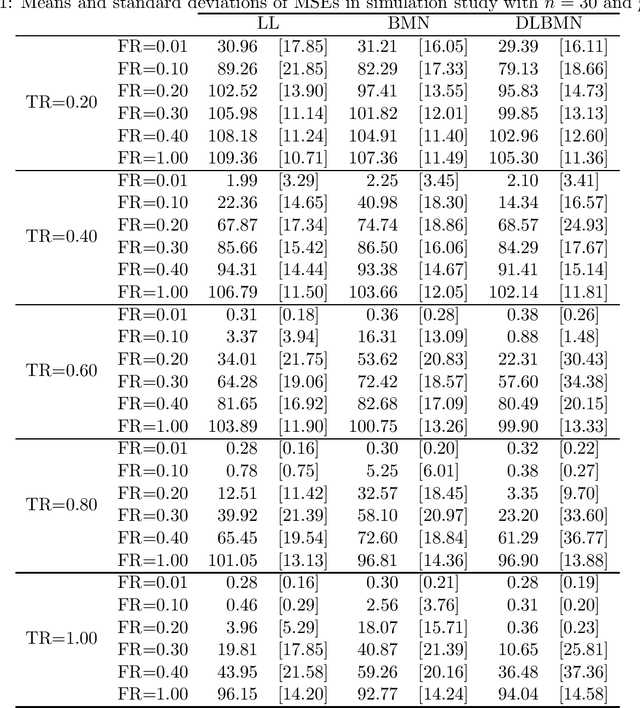
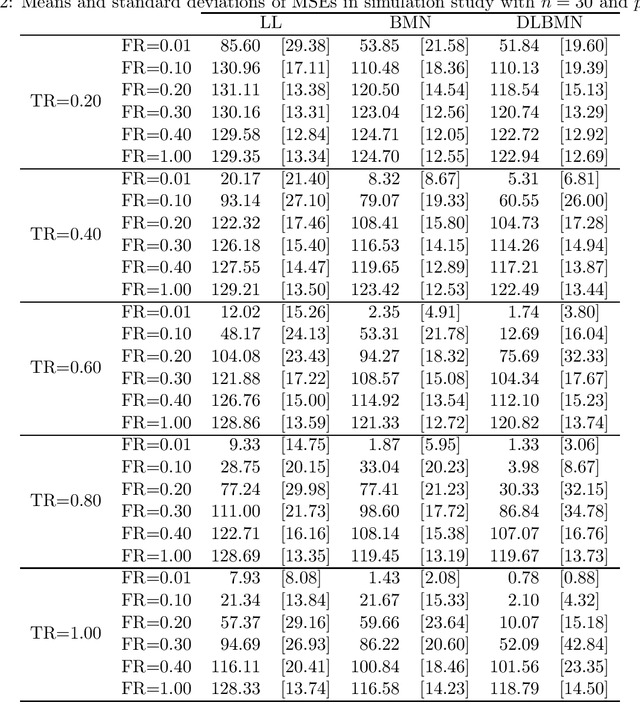
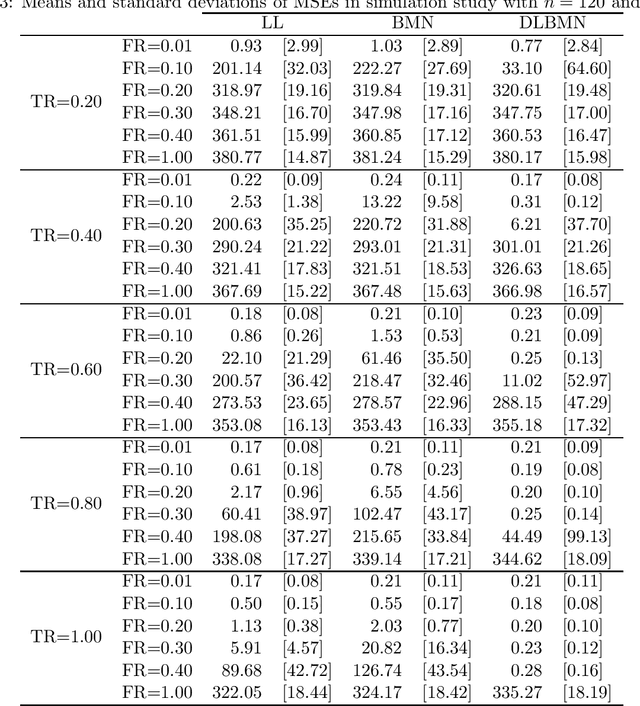
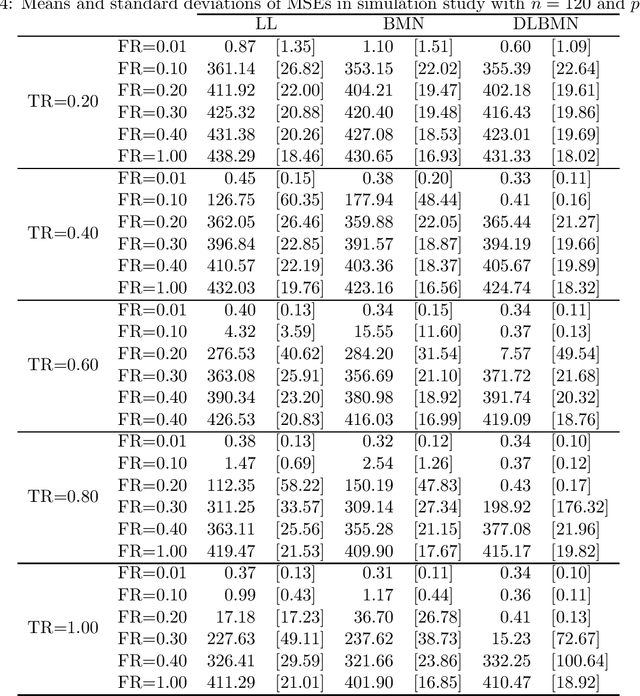
Network lasso is a method for solving a multi-task learning problem through the regularized maximum likelihood method. A characteristic of network lasso is setting a different model for each sample. The relationships among the models are represented by relational coefficients. A crucial issue in network lasso is to provide appropriate values for these relational coefficients. In this paper, we propose a Bayesian approach to solve multi-task learning problems by network lasso. This approach allows us to objectively determine the relational coefficients by Bayesian estimation. The effectiveness of the proposed method is shown in a simulation study and a real data analysis.

Multilinear Common Component Analysis via Kronecker Product Representation

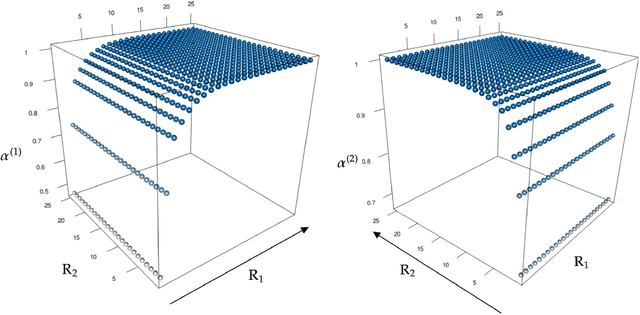
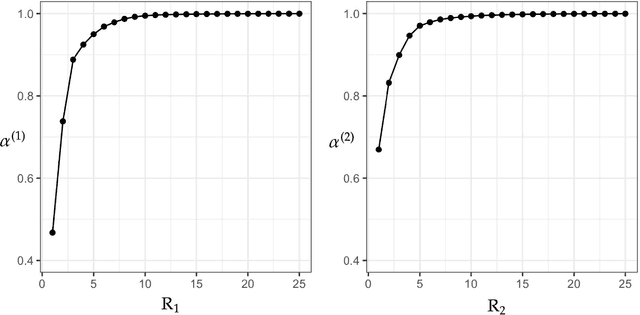
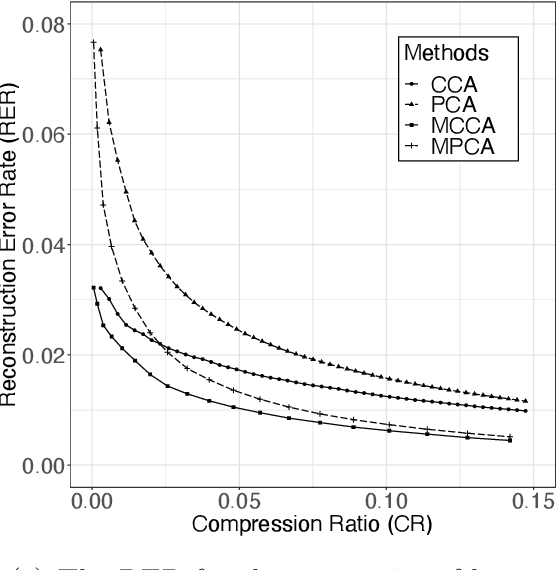
We consider the problem of extracting a common structure from multiple tensor datasets. To obtain the common structure from the multiple tensor datasets, we propose multilinear common component analysis (MCCA) based on Kronecker products of mode-wise covariance matrices. MCCA constructs the common basis represented by linear combinations of original variables without losing the information of multiple tensor datasets as possible. We also develop an estimation algorithm of MCCA that guarantees mode-wise global convergence. The numerical studies are conducted to show the effectiveness of MCCA.

Variable fusion for Bayesian linear regression via spike-and-slab priors

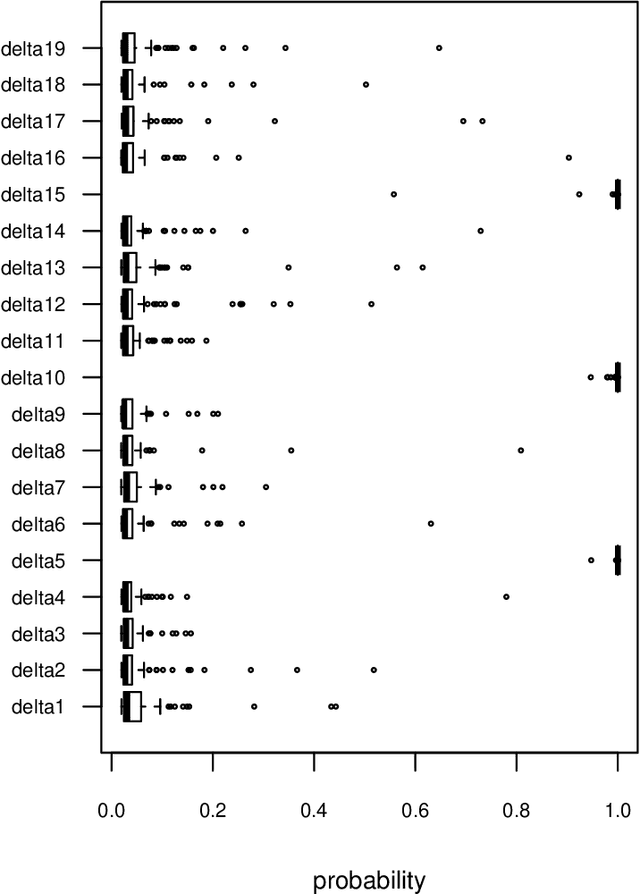
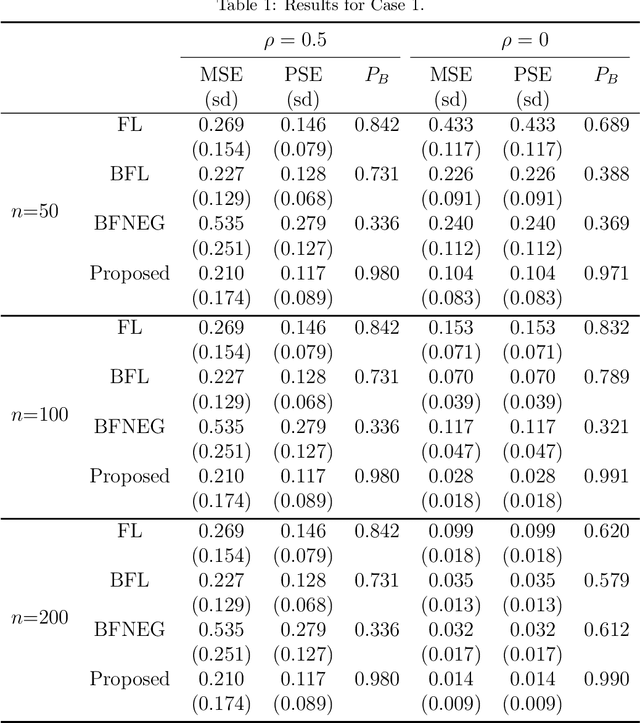
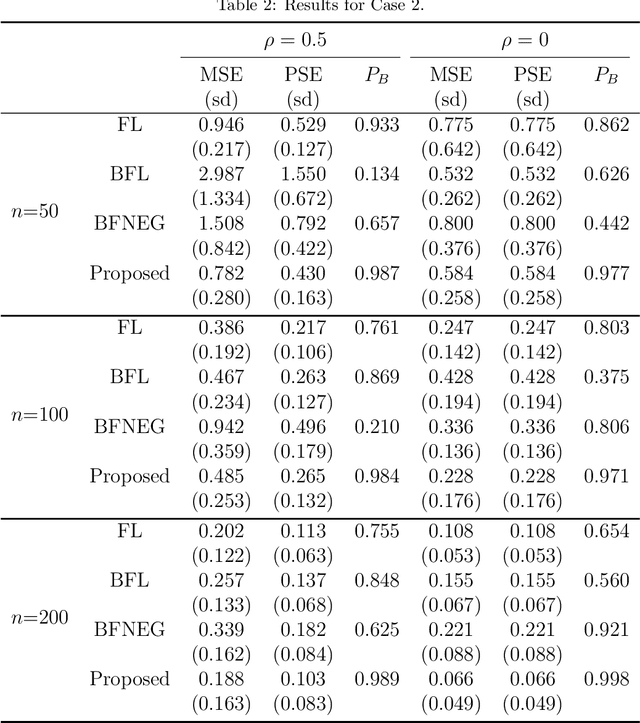
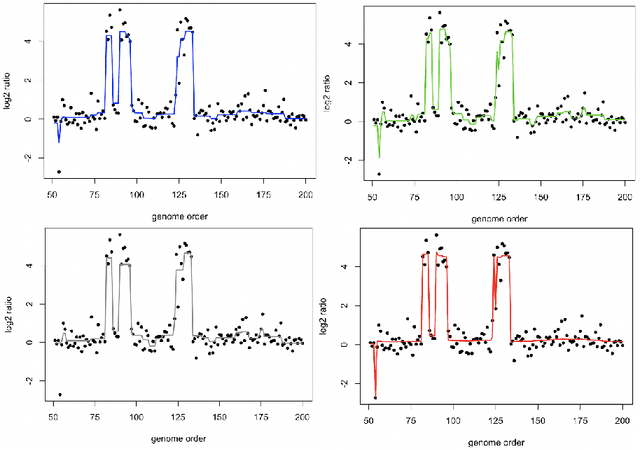
In linear regression models, a fusion of the coefficients is used to identify the predictors having similar relationships with the response. This is called variable fusion. This paper presents a novel variable fusion method in terms of Bayesian linear regression models. We focus on hierarchical Bayesian models based on a spike-and-slab prior approach. A spike-and-slab prior is designed to perform variable fusion. To obtain estimates of parameters, we develop a Gibbs sampler for the parameters. Simulation studies and a real data analysis show that our proposed method has better performances than previous methods.

Sparse principal component regression via singular value decomposition approach

Principal component regression (PCR) is a two-stage procedure: the first stage performs principal component analysis (PCA) and the second stage constructs a regression model whose explanatory variables are replaced by principal components obtained by the first stage. Since PCA is performed by using only explanatory variables, the principal components have no information about the response variable. To address the problem, we propose a one-stage procedure for PCR in terms of singular value decomposition approach. Our approach is based upon two loss functions, a regression loss and a PCA loss, with sparse regularization. The proposed method enables us to obtain principal component loadings that possess information about both explanatory variables and a response variable. An estimation algorithm is developed by using alternating direction method of multipliers. We conduct numerical studies to show the effectiveness of the proposed method.

Bayesian sparse convex clustering via global-local shrinkage priors

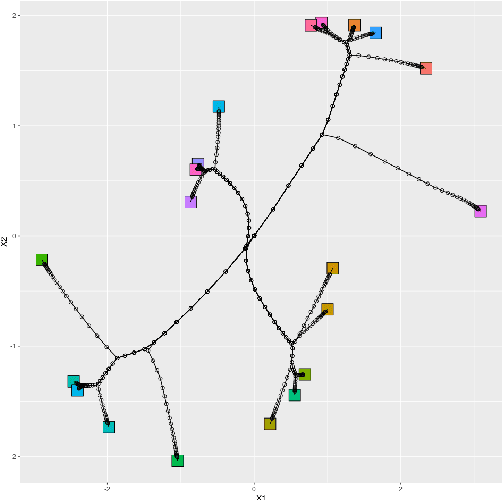
Sparse convex clustering is to cluster observations and conduct variable selection simultaneously in the framework of convex clustering. Although the weighted $L_1$ norm as the regularization term is usually employed in the sparse convex clustering, this increases the dependence on the data and reduces the estimation accuracy if the sample size is not sufficient. To tackle these problems, this paper proposes a Bayesian sparse convex clustering via the idea of Bayesian lasso and global-local shrinkage priors. We introduce Gibbs sampling algorithms for our method using scale mixtures of normals. The effectiveness of the proposed methods is shown in simulation studies and a real data analysis.