A Bayesian approach to multi-task learning with network lasso

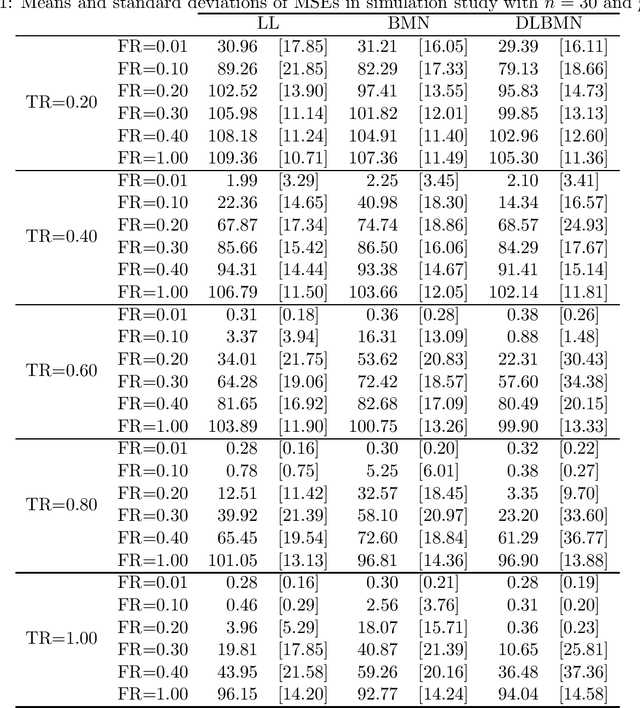
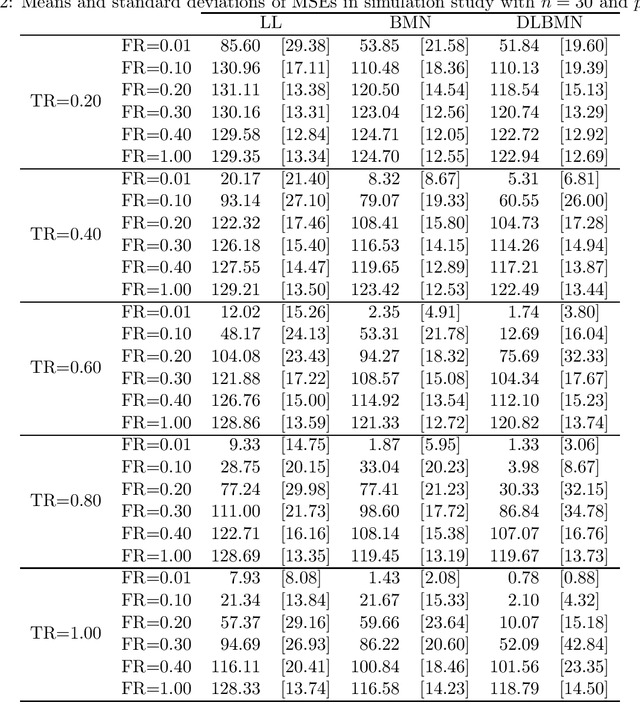
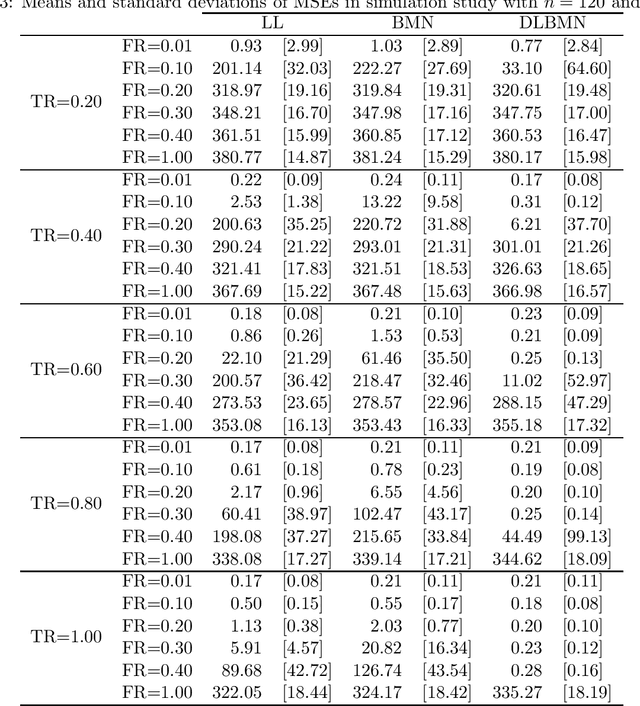
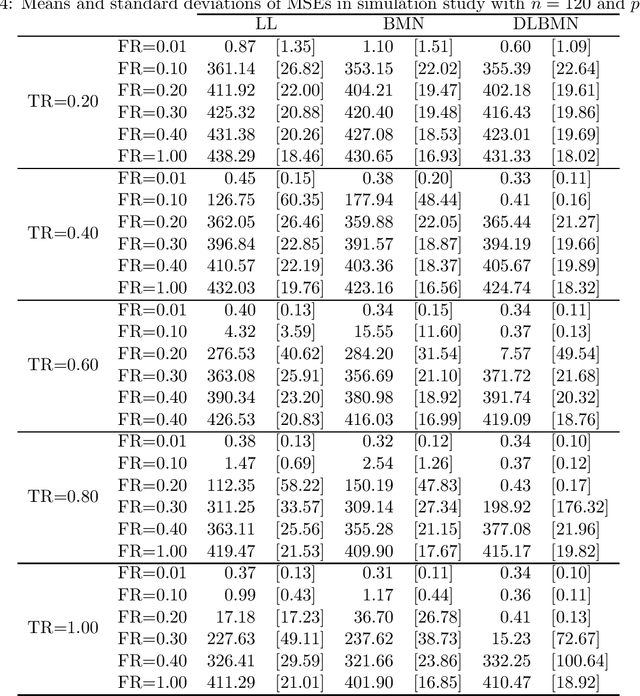
Network lasso is a method for solving a multi-task learning problem through the regularized maximum likelihood method. A characteristic of network lasso is setting a different model for each sample. The relationships among the models are represented by relational coefficients. A crucial issue in network lasso is to provide appropriate values for these relational coefficients. In this paper, we propose a Bayesian approach to solve multi-task learning problems by network lasso. This approach allows us to objectively determine the relational coefficients by Bayesian estimation. The effectiveness of the proposed method is shown in a simulation study and a real data analysis.

Variable fusion for Bayesian linear regression via spike-and-slab priors

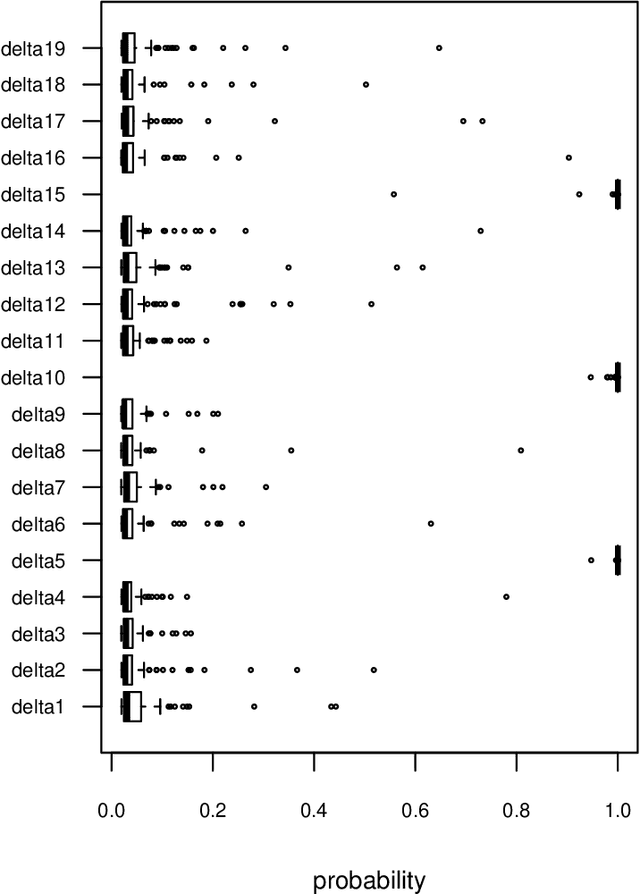
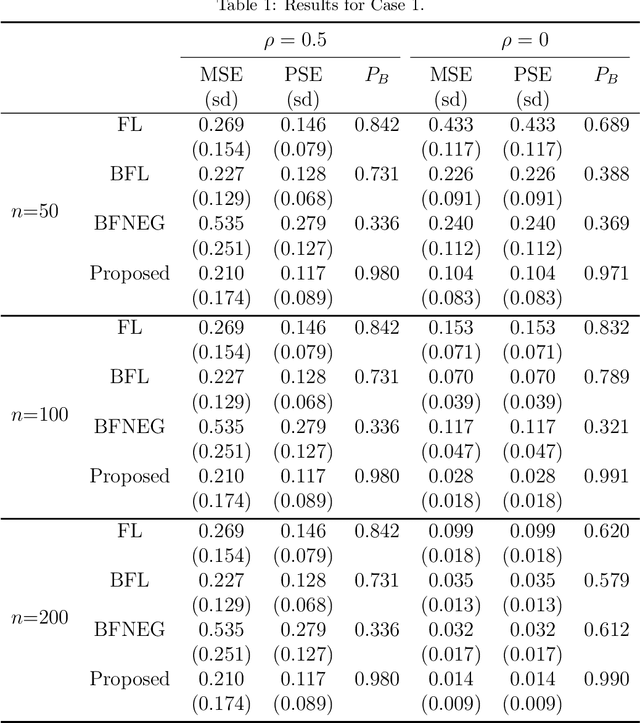
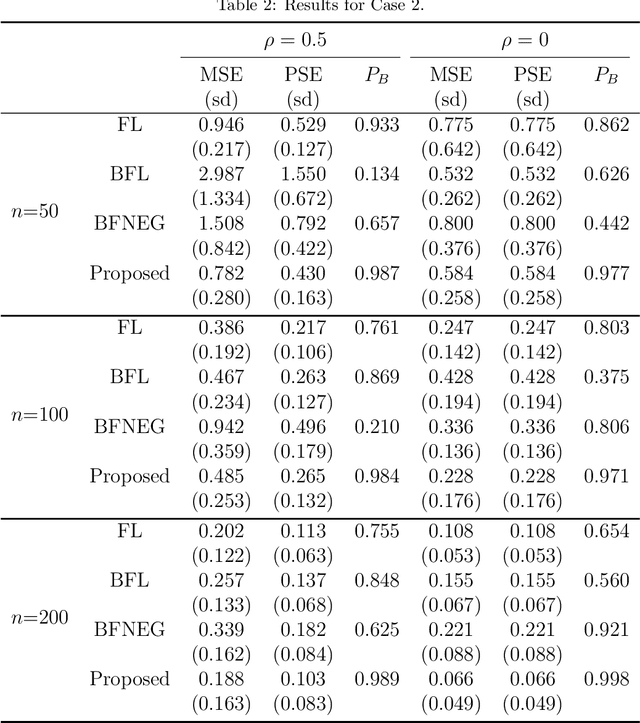
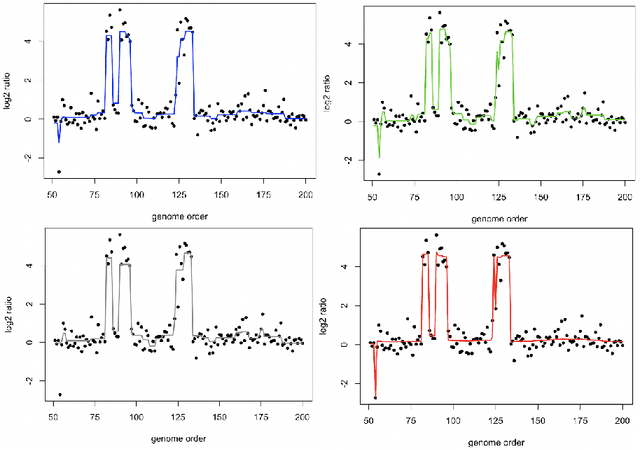
In linear regression models, a fusion of the coefficients is used to identify the predictors having similar relationships with the response. This is called variable fusion. This paper presents a novel variable fusion method in terms of Bayesian linear regression models. We focus on hierarchical Bayesian models based on a spike-and-slab prior approach. A spike-and-slab prior is designed to perform variable fusion. To obtain estimates of parameters, we develop a Gibbs sampler for the parameters. Simulation studies and a real data analysis show that our proposed method has better performances than previous methods.

Bayesian sparse convex clustering via global-local shrinkage priors

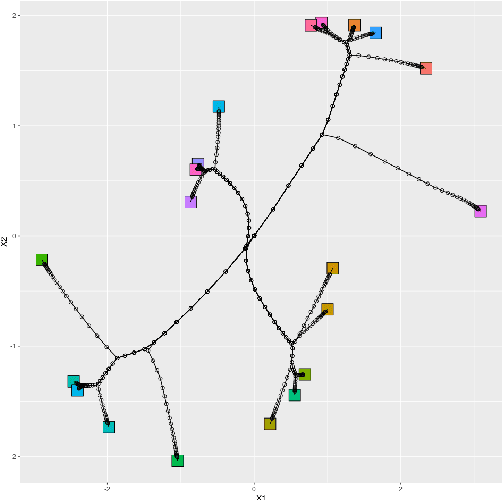
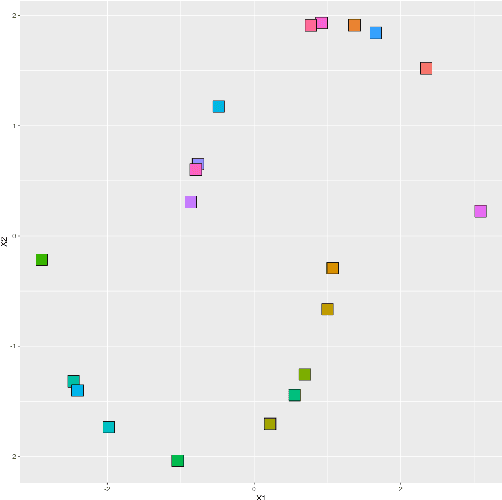
Sparse convex clustering is to cluster observations and conduct variable selection simultaneously in the framework of convex clustering. Although the weighted $L_1$ norm as the regularization term is usually employed in the sparse convex clustering, this increases the dependence on the data and reduces the estimation accuracy if the sample size is not sufficient. To tackle these problems, this paper proposes a Bayesian sparse convex clustering via the idea of Bayesian lasso and global-local shrinkage priors. We introduce Gibbs sampling algorithms for our method using scale mixtures of normals. The effectiveness of the proposed methods is shown in simulation studies and a real data analysis.

Bayesian generalized fused lasso modeling via NEG distribution

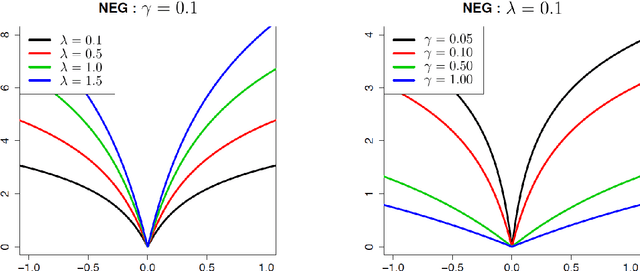
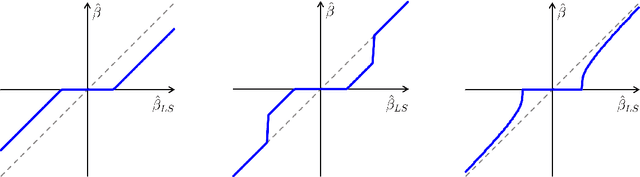
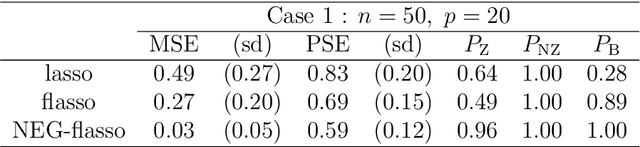
The fused lasso penalizes a loss function by the $L_1$ norm for both the regression coefficients and their successive differences to encourage sparsity of both. In this paper, we propose a Bayesian generalized fused lasso modeling based on a normal-exponential-gamma (NEG) prior distribution. The NEG prior is assumed into the difference of successive regression coefficients. The proposed method enables us to construct a more versatile sparse model than the ordinary fused lasso by using a flexible regularization term. We also propose a sparse fused algorithm to produce exact sparse solutions. Simulation studies and real data analyses show that the proposed method has superior performance to the ordinary fused lasso.