Bayesian generalized fused lasso modeling via NEG distribution
Paper and Code
Feb 16, 2016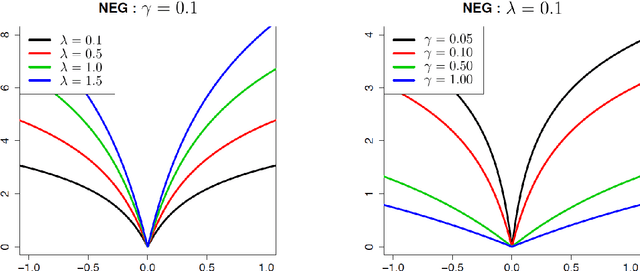

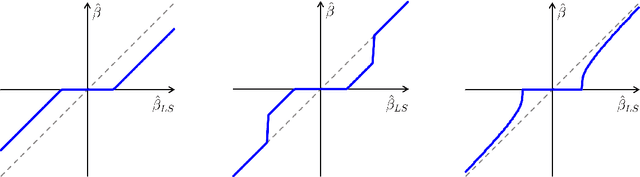
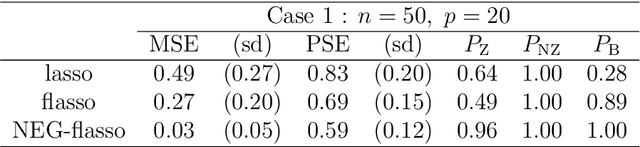
The fused lasso penalizes a loss function by the $L_1$ norm for both the regression coefficients and their successive differences to encourage sparsity of both. In this paper, we propose a Bayesian generalized fused lasso modeling based on a normal-exponential-gamma (NEG) prior distribution. The NEG prior is assumed into the difference of successive regression coefficients. The proposed method enables us to construct a more versatile sparse model than the ordinary fused lasso by using a flexible regularization term. We also propose a sparse fused algorithm to produce exact sparse solutions. Simulation studies and real data analyses show that the proposed method has superior performance to the ordinary fused lasso.
* 26 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge