Bayesian generalized fused lasso modeling via NEG distribution

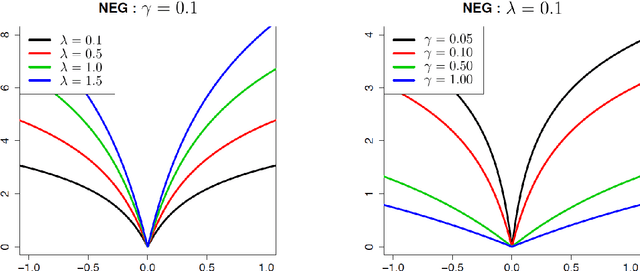
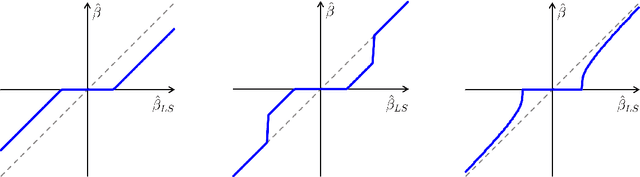
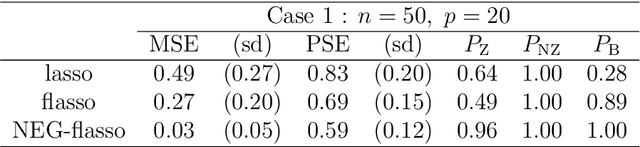
The fused lasso penalizes a loss function by the $L_1$ norm for both the regression coefficients and their successive differences to encourage sparsity of both. In this paper, we propose a Bayesian generalized fused lasso modeling based on a normal-exponential-gamma (NEG) prior distribution. The NEG prior is assumed into the difference of successive regression coefficients. The proposed method enables us to construct a more versatile sparse model than the ordinary fused lasso by using a flexible regularization term. We also propose a sparse fused algorithm to produce exact sparse solutions. Simulation studies and real data analyses show that the proposed method has superior performance to the ordinary fused lasso.

Readouts for Echo-state Networks Built using Locally Regularized Orthogonal Forward Regression

Echo state network (ESN) is viewed as a temporal non-orthogonal expansion with pseudo-random parameters. Such expansions naturally give rise to regressors of various relevance to a teacher output. We illustrate that often only a certain amount of the generated echo-regressors effectively explain the variance of the teacher output and also that sole local regularization is not able to provide in-depth information concerning the importance of the generated regressors. The importance is therefore determined by a joint calculation of the individual variance contributions and Bayesian relevance using locally regularized orthogonal forward regression (LROFR) algorithm. This information can be advantageously used in a variety of ways for an in-depth analysis of an ESN structure and its state-space parameters in relation to the unknown dynamics of the underlying problem. We present locally regularized linear readout built using LROFR. The readout may have a different dimensionality than an ESN model itself, and besides improving robustness and accuracy of an ESN it relates the echo-regressors to different features of the training data and may determine what type of an additional readout is suitable for a task at hand. Moreover, as flexibility of the linear readout has limitations and might sometimes be insufficient for certain tasks, we also present a radial basis function (RBF) readout built using LROFR. It is a flexible and parsimonious readout with excellent generalization abilities and is a viable alternative to readouts based on a feed-forward neural network (FFNN) or an RBF net built using relevance vector machine (RVM).

Semi-supervised logistic discrimination for functional data

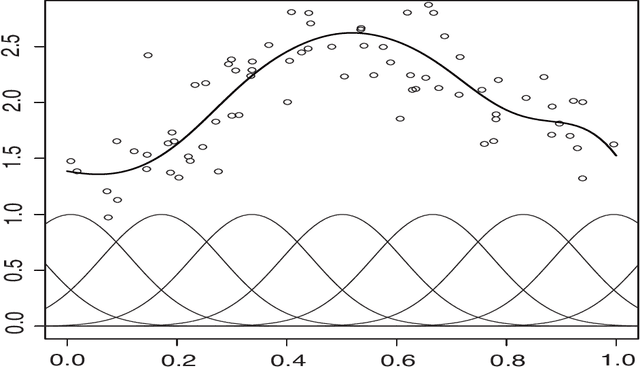
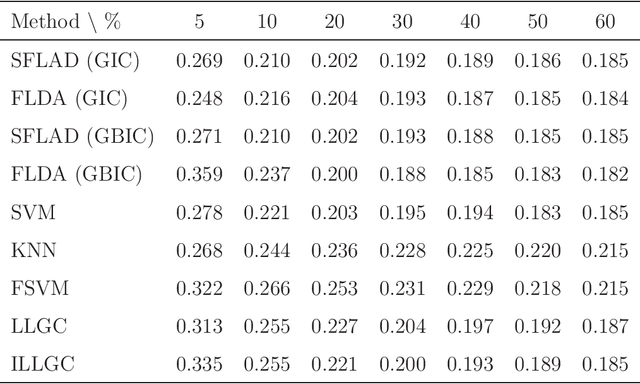
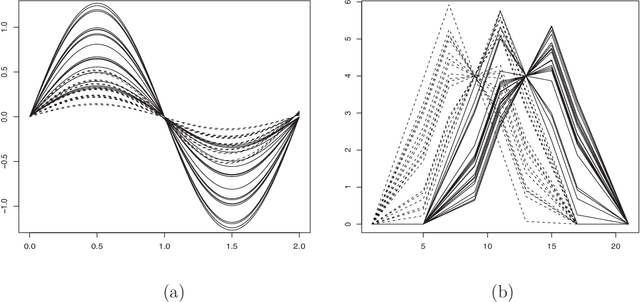
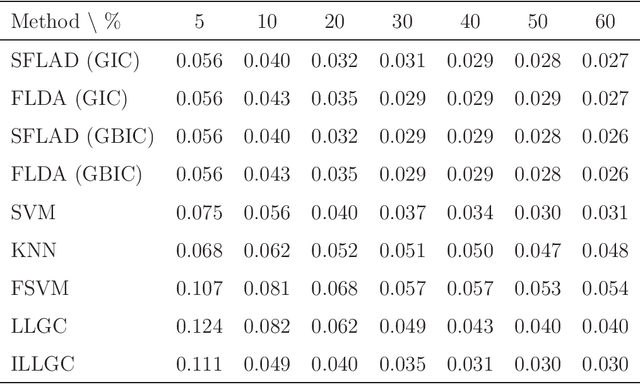
Multi-class classification methods based on both labeled and unlabeled functional data sets are discussed. We present a semi-supervised logistic model for classification in the context of functional data analysis. Unknown parameters in our proposed model are estimated by regularization with the help of EM algorithm. A crucial point in the modeling procedure is the choice of a regularization parameter involved in the semi-supervised functional logistic model. In order to select the adjusted parameter, we introduce model selection criteria from information-theoretic and Bayesian viewpoints. Monte Carlo simulations and a real data analysis are given to examine the effectiveness of our proposed modeling strategy.

Efficient algorithm to select tuning parameters in sparse regression modeling with regularization

In sparse regression modeling via regularization such as the lasso, it is important to select appropriate values of tuning parameters including regularization parameters. The choice of tuning parameters can be viewed as a model selection and evaluation problem. Mallows' $C_p$ type criteria may be used as a tuning parameter selection tool in lasso-type regularization methods, for which the concept of degrees of freedom plays a key role. In the present paper, we propose an efficient algorithm that computes the degrees of freedom by extending the generalized path seeking algorithm. Our procedure allows us to construct model selection criteria for evaluating models estimated by regularization with a wide variety of convex and non-convex penalties. Monte Carlo simulations demonstrate that our methodology performs well in various situations. A real data example is also given to illustrate our procedure.