Bayesian sparse convex clustering via global-local shrinkage priors

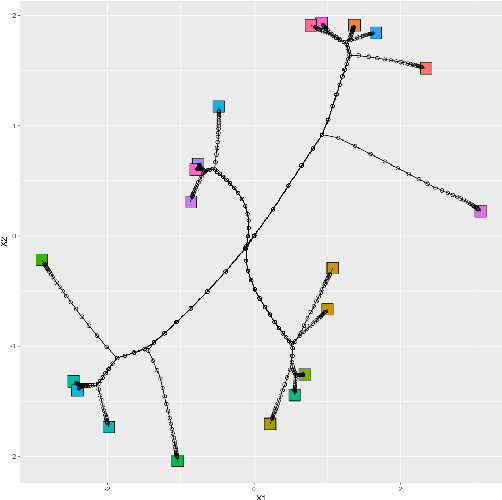
Sparse convex clustering is to cluster observations and conduct variable selection simultaneously in the framework of convex clustering. Although the weighted $L_1$ norm as the regularization term is usually employed in the sparse convex clustering, this increases the dependence on the data and reduces the estimation accuracy if the sample size is not sufficient. To tackle these problems, this paper proposes a Bayesian sparse convex clustering via the idea of Bayesian lasso and global-local shrinkage priors. We introduce Gibbs sampling algorithms for our method using scale mixtures of normals. The effectiveness of the proposed methods is shown in simulation studies and a real data analysis.