Multilinear Common Component Analysis via Kronecker Product Representation

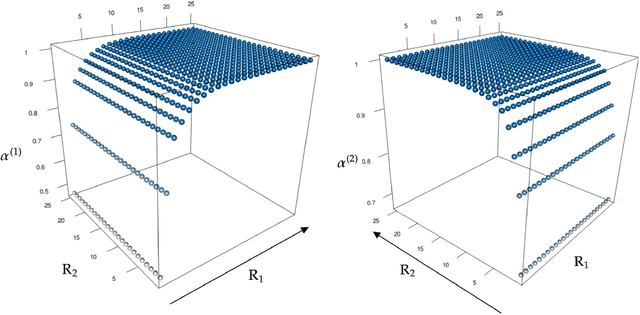
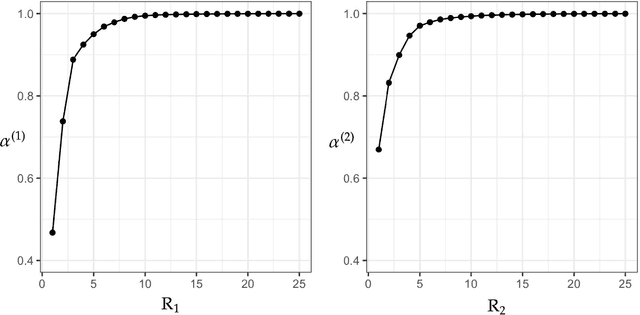
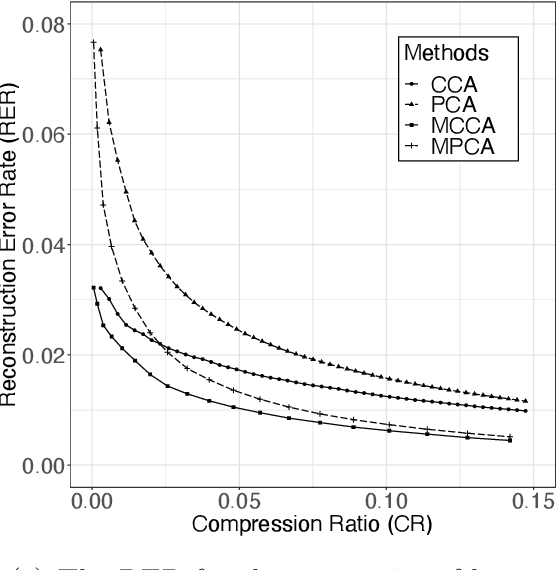
We consider the problem of extracting a common structure from multiple tensor datasets. To obtain the common structure from the multiple tensor datasets, we propose multilinear common component analysis (MCCA) based on Kronecker products of mode-wise covariance matrices. MCCA constructs the common basis represented by linear combinations of original variables without losing the information of multiple tensor datasets as possible. We also develop an estimation algorithm of MCCA that guarantees mode-wise global convergence. The numerical studies are conducted to show the effectiveness of MCCA.

Variable fusion for Bayesian linear regression via spike-and-slab priors

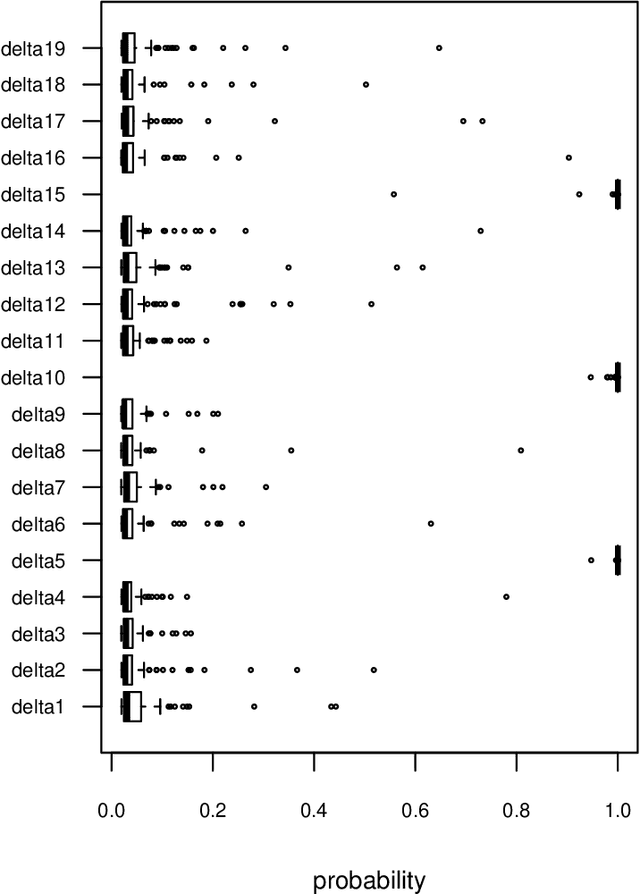
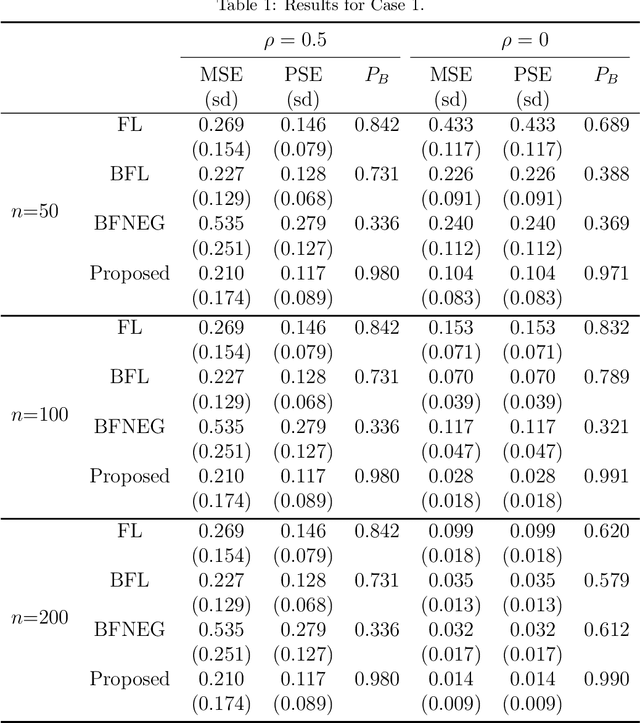
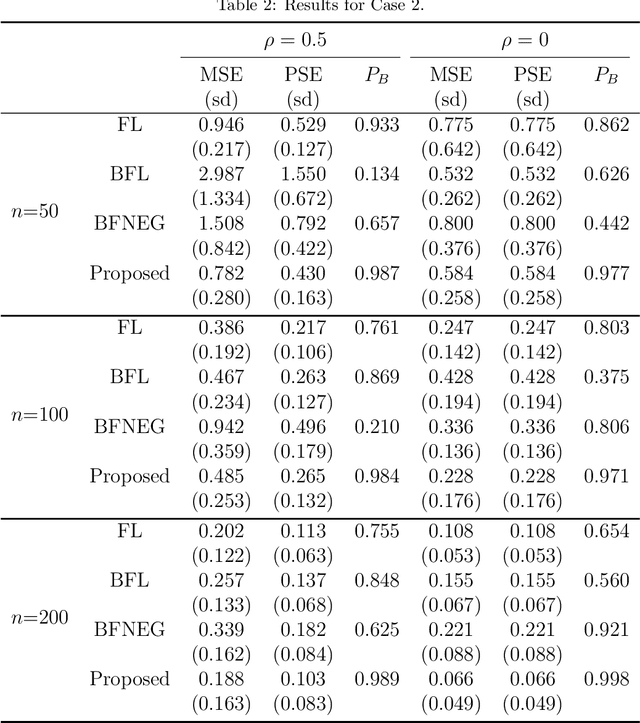
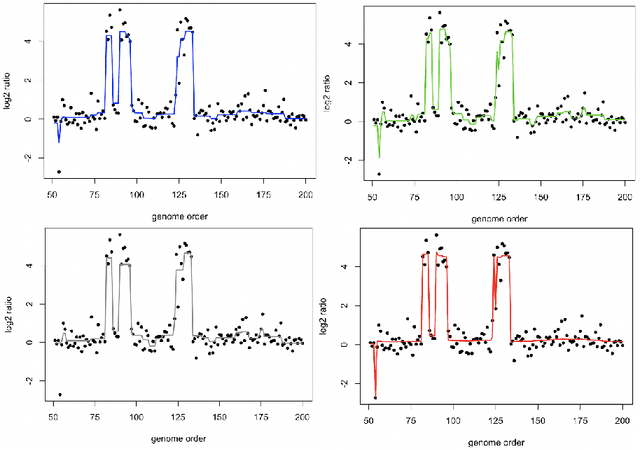
In linear regression models, a fusion of the coefficients is used to identify the predictors having similar relationships with the response. This is called variable fusion. This paper presents a novel variable fusion method in terms of Bayesian linear regression models. We focus on hierarchical Bayesian models based on a spike-and-slab prior approach. A spike-and-slab prior is designed to perform variable fusion. To obtain estimates of parameters, we develop a Gibbs sampler for the parameters. Simulation studies and a real data analysis show that our proposed method has better performances than previous methods.

Sparse Reduced-Rank Regression for Simultaneous Rank and Variable Selection via Manifold Optimization

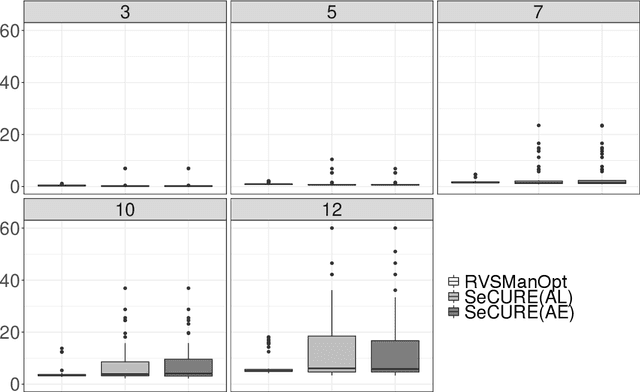
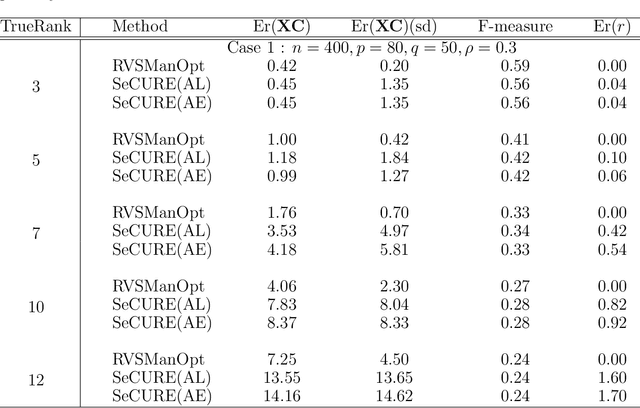
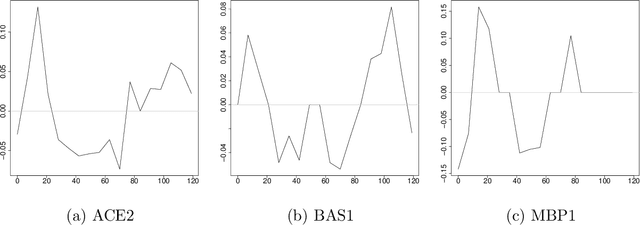
We consider the problem of constructing a reduced-rank regression model whose coefficient parameter is represented as a singular value decomposition with sparse singular vectors. The traditional estimation procedure for the coefficient parameter often fails when the true rank of the parameter is high. To overcome this issue, we develop an estimation algorithm with rank and variable selection via sparse regularization and manifold optimization, which enables us to obtain an accurate estimation of the coefficient parameter even if the true rank of the coefficient parameter is high. Using sparse regularization, we can also select an optimal value of the rank. We conduct Monte Carlo experiments and real data analysis to illustrate the effectiveness of our proposed method.