Sparse Reduced-Rank Regression for Simultaneous Rank and Variable Selection via Manifold Optimization
Paper and Code
Nov 01, 2019
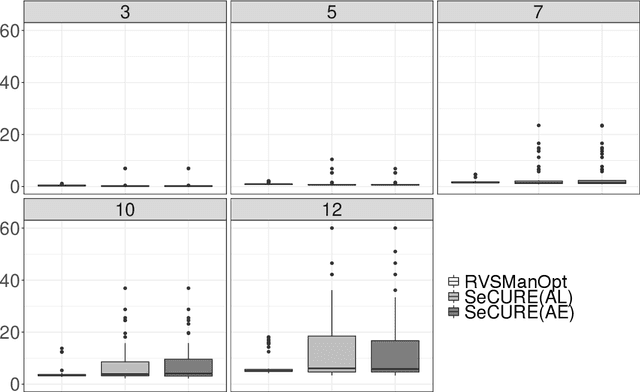
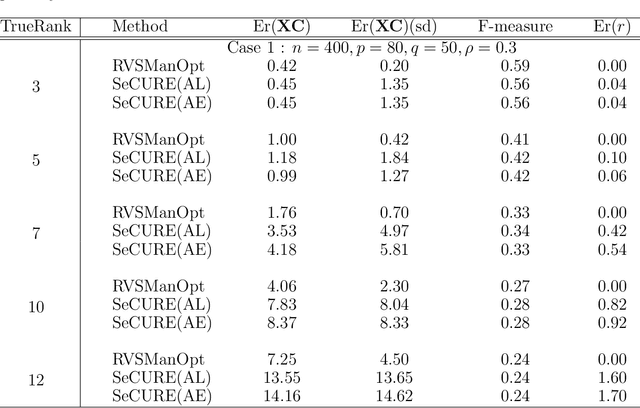
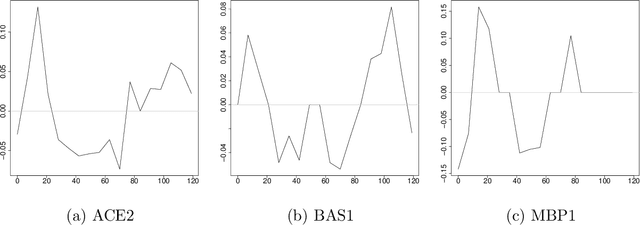
We consider the problem of constructing a reduced-rank regression model whose coefficient parameter is represented as a singular value decomposition with sparse singular vectors. The traditional estimation procedure for the coefficient parameter often fails when the true rank of the parameter is high. To overcome this issue, we develop an estimation algorithm with rank and variable selection via sparse regularization and manifold optimization, which enables us to obtain an accurate estimation of the coefficient parameter even if the true rank of the coefficient parameter is high. Using sparse regularization, we can also select an optimal value of the rank. We conduct Monte Carlo experiments and real data analysis to illustrate the effectiveness of our proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge