Sparse principal component regression via singular value decomposition approach
Paper and Code
Feb 21, 2020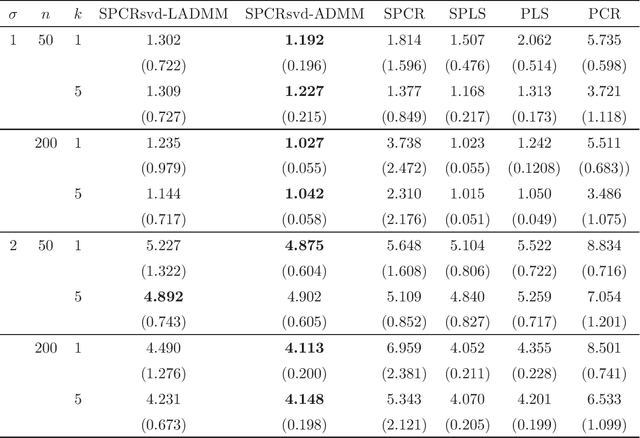
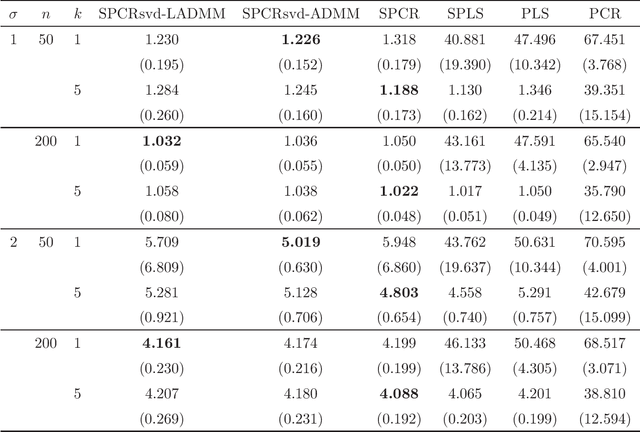
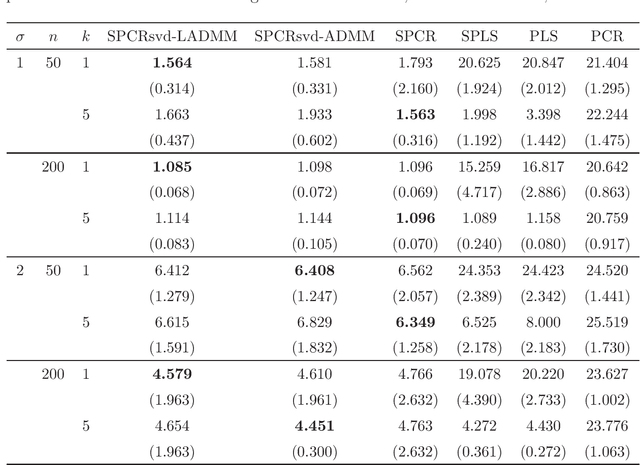
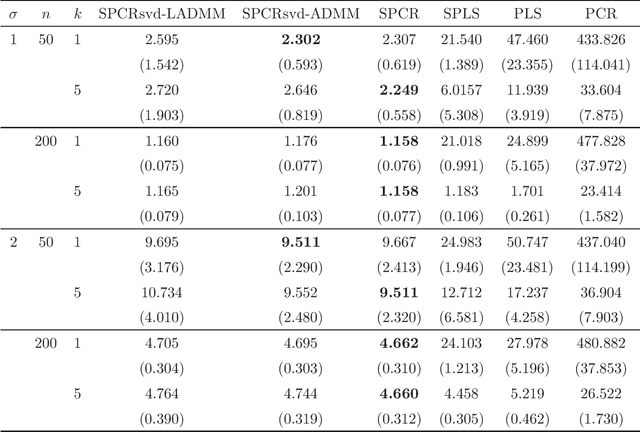
Principal component regression (PCR) is a two-stage procedure: the first stage performs principal component analysis (PCA) and the second stage constructs a regression model whose explanatory variables are replaced by principal components obtained by the first stage. Since PCA is performed by using only explanatory variables, the principal components have no information about the response variable. To address the problem, we propose a one-stage procedure for PCR in terms of singular value decomposition approach. Our approach is based upon two loss functions, a regression loss and a PCA loss, with sparse regularization. The proposed method enables us to obtain principal component loadings that possess information about both explanatory variables and a response variable. An estimation algorithm is developed by using alternating direction method of multipliers. We conduct numerical studies to show the effectiveness of the proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge