TOT: Topology-Aware Optimal Transport For Multimodal Hate Detection

Multimodal hate detection, which aims to identify harmful content online such as memes, is crucial for building a wholesome internet environment. Previous work has made enlightening exploration in detecting explicit hate remarks. However, most of their approaches neglect the analysis of implicit harm, which is particularly challenging as explicit text markers and demographic visual cues are often twisted or missing. The leveraged cross-modal attention mechanisms also suffer from the distributional modality gap and lack logical interpretability. To address these semantic gaps issues, we propose TOT: a topology-aware optimal transport framework to decipher the implicit harm in memes scenario, which formulates the cross-modal aligning problem as solutions for optimal transportation plans. Specifically, we leverage an optimal transport kernel method to capture complementary information from multiple modalities. The kernel embedding provides a non-linear transformation ability to reproduce a kernel Hilbert space (RKHS), which reflects significance for eliminating the distributional modality gap. Moreover, we perceive the topology information based on aligned representations to conduct bipartite graph path reasoning. The newly achieved state-of-the-art performance on two publicly available benchmark datasets, together with further visual analysis, demonstrate the superiority of TOT in capturing implicit cross-modal alignment.

HYPER^2: Hyperbolic Poincare Embedding for Hyper-Relational Link Prediction

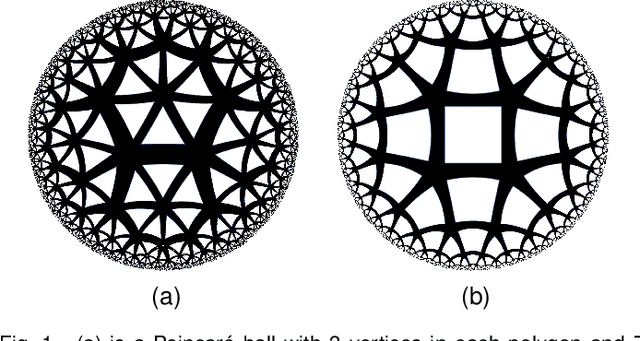
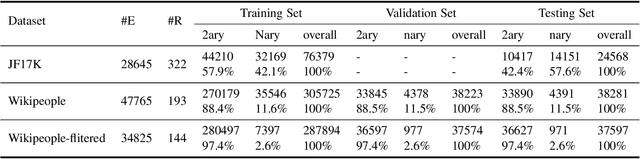
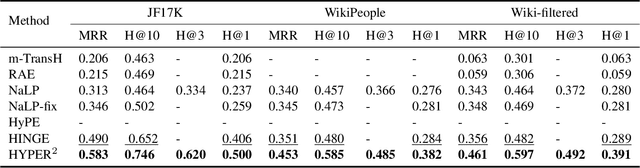
Link Prediction, addressing the issue of completing KGs with missing facts, has been broadly studied. However, less light is shed on the ubiquitous hyper-relational KGs. Most existing hyper-relational KG embedding models still tear an n-ary fact into smaller tuples, neglecting the indecomposability of some n-ary facts. While other frameworks work for certain arity facts only or ignore the significance of primary triple. In this paper, we represent an n-ary fact as a whole, simultaneously keeping the integrity of n-ary fact and maintaining the vital role that the primary triple plays. In addition, we generalize hyperbolic Poincar\'e embedding from binary to arbitrary arity data, which has not been studied yet. To tackle the weak expressiveness and high complexity issue, we propose HYPER^2 which is qualified for capturing the interaction between entities within and beyond triple through information aggregation on the tangent space. Extensive experiments demonstrate HYPER^2 achieves superior performance to its translational and deep analogues, improving SOTA by up to 34.5\% with relatively few dimensions. Moreover, we study the side effect of literals and we theoretically and experimentally compare the computational complexity of HYPER^2 against several best performing baselines, HYPER^2 is 49-61 times quicker than its counterparts.