Triply Laplacian Scale Mixture Modeling for Seismic Data Noise Suppression

Sparsity-based tensor recovery methods have shown great potential in suppressing seismic data noise. These methods exploit tensor sparsity measures capturing the low-dimensional structures inherent in seismic data tensors to remove noise by applying sparsity constraints through soft-thresholding or hard-thresholding operators. However, in these methods, considering that real seismic data are non-stationary and affected by noise, the variances of tensor coefficients are unknown and may be difficult to accurately estimate from the degraded seismic data, leading to undesirable noise suppression performance. In this paper, we propose a novel triply Laplacian scale mixture (TLSM) approach for seismic data noise suppression, which significantly improves the estimation accuracy of both the sparse tensor coefficients and hidden scalar parameters. To make the optimization problem manageable, an alternating direction method of multipliers (ADMM) algorithm is employed to solve the proposed TLSM-based seismic data noise suppression problem. Extensive experimental results on synthetic and field seismic data demonstrate that the proposed TLSM algorithm outperforms many state-of-the-art seismic data noise suppression methods in both quantitative and qualitative evaluations while providing exceptional computational efficiency.

4-D Epanechnikov Mixture Regression in Light Field Image Compression

With the emergence of light field imaging in recent years, the compression of its elementary image array (EIA) has become a significant problem. Our coding framework includes modeling and reconstruction. For the modeling, the covariance-matrix form of the 4-D Epanechnikov kernel (4-D EK) and its correlated statistics were deduced to obtain the 4-D Epanechnikov mixture models (4-D EMMs). A 4-D Epanechnikov mixture regression (4-D EMR) was proposed based on this 4-D EK, and a 4-D adaptive model selection (4-D AMLS) algorithm was designed to realize the optimal modeling for a pseudo video sequence (PVS) of the extracted key-EIA. A linear function based reconstruction (LFBR) was proposed based on the correlation between adjacent elementary images (EIs). The decoded images realized a clear outline reconstruction and superior coding efficiency compared to high-efficiency video coding (HEVC) and JPEG 2000 below approximately 0.05 bpp. This work realized an unprecedented theoretical application by (1) proposing the 4-D Epanechnikov kernel theory, (2) exploiting the 4-D Epanechnikov mixture regression and its application in the modeling of the pseudo video sequence of light field images, (3) using 4-D adaptive model selection for the optimal number of models, and (4) employing a linear function-based reconstruction according to the content similarity.

Three-dimensional Epanechnikov mixture regression in image coding

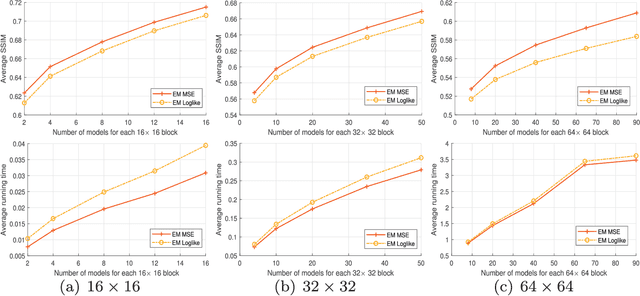
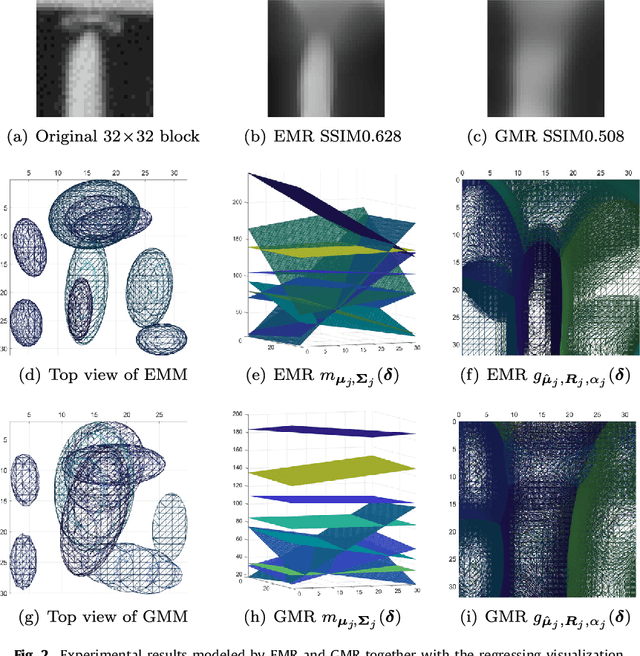
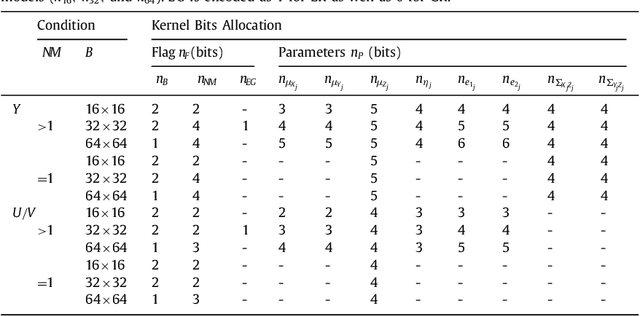
Kernel methods have been studied extensively in recent years. We propose a three-dimensional (3-D) Epanechnikov Mixture Regression (EMR) based on our Epanechnikov Kernel (EK) and realize a complete framework for image coding. In our research, we deduce the covariance-matrix form of 3-D Epanechnikov kernels and their correlated statistics to obtain the Epanechnikov mixture models. To apply our theories to image coding, we propose the 3-D EMR which can better model an image in smaller blocks compared with the conventional Gaussian Mixture Regression (GMR). The regressions are all based on our improved Expectation-Maximization (EM) algorithm with mean square error optimization. Finally, we design an Adaptive Mode Selection (AMS) algorithm to realize the best model pattern combination for coding. Our recovered image has clear outlines and superior coding efficiency compared to JPEG below 0.25bpp. Our work realizes an unprecedented theory application by: (1) enriching the theory of Epanechnikov kernel,(2) improving the EM algorithm using MSE optimization, (3) exploiting the EMR and its application in image coding, and (4) AMS optimal modeling combined with Gaussian and Epanechnikov kernel.