Composable Core-sets for Determinant Maximization: A Simple Near-Optimal Algorithm

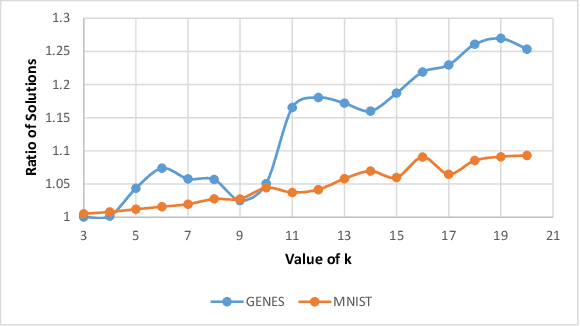
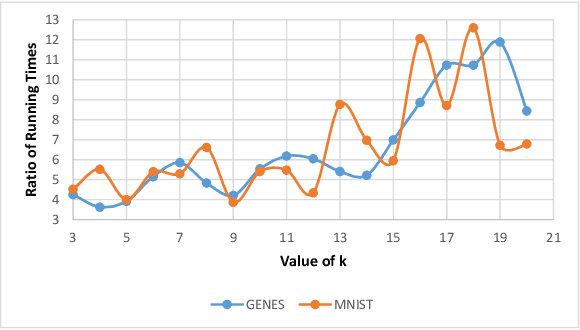
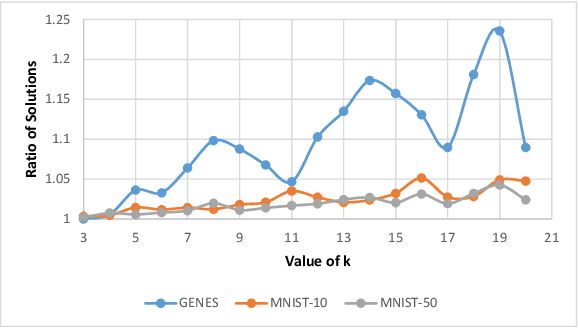
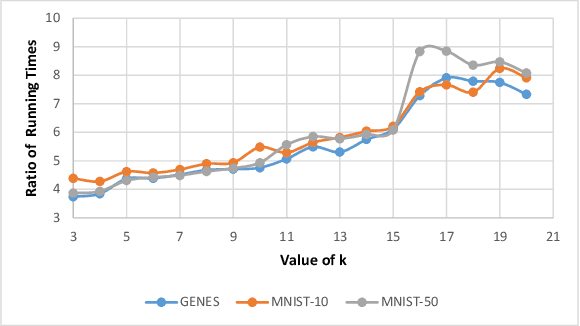
``Composable core-sets'' are an efficient framework for solving optimization problems in massive data models. In this work, we consider efficient construction of composable core-sets for the determinant maximization problem. This can also be cast as the MAP inference task for determinantal point processes, that have recently gained a lot of interest for modeling diversity and fairness. The problem was recently studied in [IMOR'18], where they designed composable core-sets with the optimal approximation bound of $\tilde O(k)^k$. On the other hand, the more practical Greedy algorithm has been previously used in similar contexts. In this work, first we provide a theoretical approximation guarantee of $O(C^{k^2})$ for the Greedy algorithm in the context of composable core-sets; Further, we propose to use a Local Search based algorithm that while being still practical, achieves a nearly optimal approximation bound of $O(k)^{2k}$; Finally, we implement all three algorithms and show the effectiveness of our proposed algorithm on standard data sets.

A Polynomial Time MCMC Method for Sampling from Continuous DPPs

We study the Gibbs sampling algorithm for continuous determinantal point processes. We show that, given a warm start, the Gibbs sampler generates a random sample from a continuous $k$-DPP defined on a $d$-dimensional domain by only taking $\text{poly}(k)$ number of steps. As an application, we design an algorithm to generate random samples from $k$-DPPs defined by a spherical Gaussian kernel on a unit sphere in $d$-dimensions, $\mathbb{S}^{d-1}$ in time polynomial in $k,d$.

Composable Core-sets for Determinant Maximization Problems via Spectral Spanners

We study a spectral generalization of classical combinatorial graph spanners to the spectral setting. Given a set of vectors $V\subseteq \Re^d$, we say a set $U\subseteq V$ is an $\alpha$-spectral spanner if for all $v\in V$ there is a probability distribution $\mu_v$ supported on $U$ such that $$vv^\intercal \preceq \alpha\cdot\mathbb{E}_{u\sim\mu_v} uu^\intercal.$$ We show that any set $V$ has an $\tilde{O}(d)$-spectral spanner of size $\tilde{O}(d)$ and this bound is almost optimal in the worst case. We use spectral spanners to study composable core-sets for spectral problems. We show that for many objective functions one can use a spectral spanner, independent of the underlying functions, as a core-set and obtain almost optimal composable core-sets. For example, for the determinant maximization problem we obtain an $\tilde{O}(k)^k$-composable core-set and we show that this is almost optimal in the worst case. Our algorithm is a spectral analogue of the classical greedy algorithm for finding (combinatorial) spanners in graphs. We expect that our spanners find many other applications in distributed or parallel models of computation. Our proof is spectral. As a side result of our techniques, we show that the rank of diagonally dominant lower-triangular matrices are robust under `small perturbations' which could be of independent interests.

Time-Space Tradeoffs for Learning from Small Test Spaces: Learning Low Degree Polynomial Functions

We develop an extension of recently developed methods for obtaining time-space tradeoff lower bounds for problems of learning from random test samples to handle the situation where the space of tests is signficantly smaller than the space of inputs, a class of learning problems that is not handled by prior work. This extension is based on a measure of how matrices amplify the 2-norms of probability distributions that is more refined than the 2-norms of these matrices. As applications that follow from our new technique, we show that any algorithm that learns $m$-variate homogeneous polynomial functions of degree at most $d$ over $\mathbb{F}_2$ from evaluations on randomly chosen inputs either requires space $\Omega(mn)$ or $2^{\Omega(m)}$ time where $n=m^{\Theta(d)}$ is the dimension of the space of such functions. These bounds are asymptotically optimal since they match the tradeoffs achieved by natural learning algorithms for the problems.

Monte Carlo Markov Chain Algorithms for Sampling Strongly Rayleigh Distributions and Determinantal Point Processes

Strongly Rayleigh distributions are natural generalizations of product and determinantal probability distributions and satisfy strongest form of negative dependence properties. We show that the "natural" Monte Carlo Markov Chain (MCMC) is rapidly mixing in the support of a {\em homogeneous} strongly Rayleigh distribution. As a byproduct, our proof implies Markov chains can be used to efficiently generate approximate samples of a $k$-determinantal point process. This answers an open question raised by Deshpande and Rademacher.

Partitioning into Expanders

Let G=(V,E) be an undirected graph, lambda_k be the k-th smallest eigenvalue of the normalized laplacian matrix of G. There is a basic fact in algebraic graph theory that lambda_k > 0 if and only if G has at most k-1 connected components. We prove a robust version of this fact. If lambda_k>0, then for some 1\leq \ell\leq k-1, V can be {\em partitioned} into l sets P_1,\ldots,P_l such that each P_i is a low-conductance set in G and induces a high conductance induced subgraph. In particular, \phi(P_i)=O(l^3\sqrt{\lambda_l}) and \phi(G[P_i]) >= \lambda_k/k^2). We make our results algorithmic by designing a simple polynomial time spectral algorithm to find such partitioning of G with a quadratic loss in the inside conductance of P_i's. Unlike the recent results on higher order Cheeger's inequality [LOT12,LRTV12], our algorithmic results do not use higher order eigenfunctions of G. If there is a sufficiently large gap between lambda_k and lambda_{k+1}, more precisely, if \lambda_{k+1} >= \poly(k) lambda_{k}^{1/4} then our algorithm finds a k partitioning of V into sets P_1,...,P_k such that the induced subgraph G[P_i] has a significantly larger conductance than the conductance of P_i in G. Such a partitioning may represent the best k clustering of G. Our algorithm is a simple local search that only uses the Spectral Partitioning algorithm as a subroutine. We expect to see further applications of this simple algorithm in clustering applications.

Improved Cheeger's Inequality: Analysis of Spectral Partitioning Algorithms through Higher Order Spectral Gap

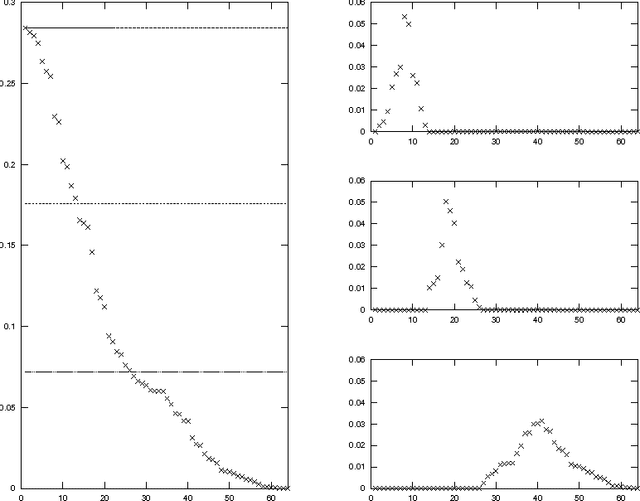
Let \phi(G) be the minimum conductance of an undirected graph G, and let 0=\lambda_1 <= \lambda_2 <=... <= \lambda_n <= 2 be the eigenvalues of the normalized Laplacian matrix of G. We prove that for any graph G and any k >= 2, \phi(G) = O(k) \lambda_2 / \sqrt{\lambda_k}, and this performance guarantee is achieved by the spectral partitioning algorithm. This improves Cheeger's inequality, and the bound is optimal up to a constant factor for any k. Our result shows that the spectral partitioning algorithm is a constant factor approximation algorithm for finding a sparse cut if \lambda_k$ is a constant for some constant k. This provides some theoretical justification to its empirical performance in image segmentation and clustering problems. We extend the analysis to other graph partitioning problems, including multi-way partition, balanced separator, and maximum cut.