Composable Core-sets for Determinant Maximization: A Simple Near-Optimal Algorithm
Paper and Code
Jul 06, 2019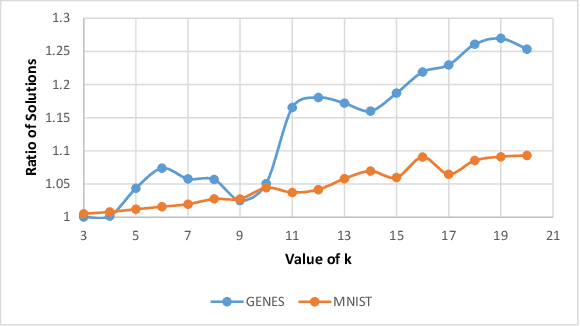
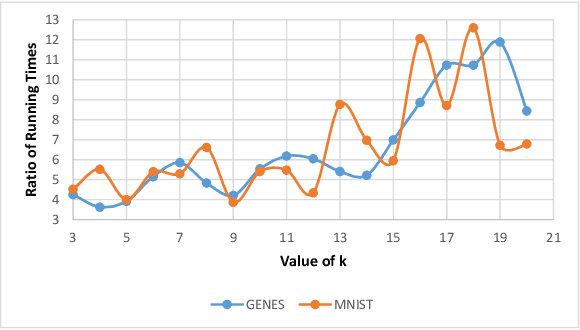
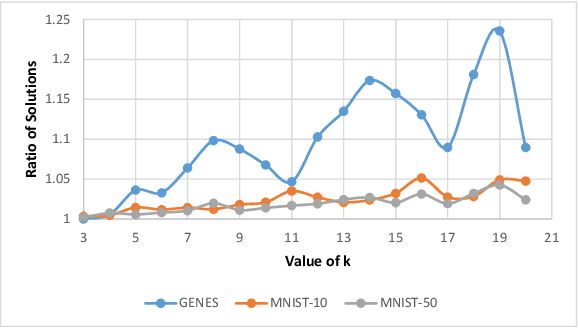
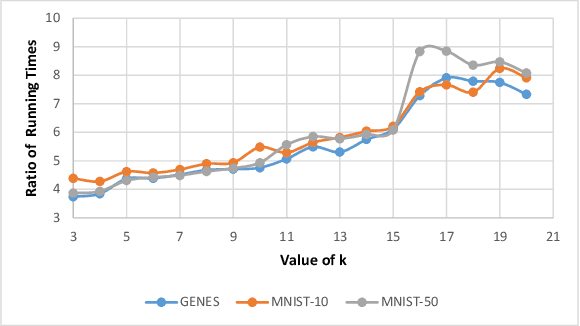
``Composable core-sets'' are an efficient framework for solving optimization problems in massive data models. In this work, we consider efficient construction of composable core-sets for the determinant maximization problem. This can also be cast as the MAP inference task for determinantal point processes, that have recently gained a lot of interest for modeling diversity and fairness. The problem was recently studied in [IMOR'18], where they designed composable core-sets with the optimal approximation bound of $\tilde O(k)^k$. On the other hand, the more practical Greedy algorithm has been previously used in similar contexts. In this work, first we provide a theoretical approximation guarantee of $O(C^{k^2})$ for the Greedy algorithm in the context of composable core-sets; Further, we propose to use a Local Search based algorithm that while being still practical, achieves a nearly optimal approximation bound of $O(k)^{2k}$; Finally, we implement all three algorithms and show the effectiveness of our proposed algorithm on standard data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge