LaTiM: Longitudinal representation learning in continuous-time models to predict disease progression

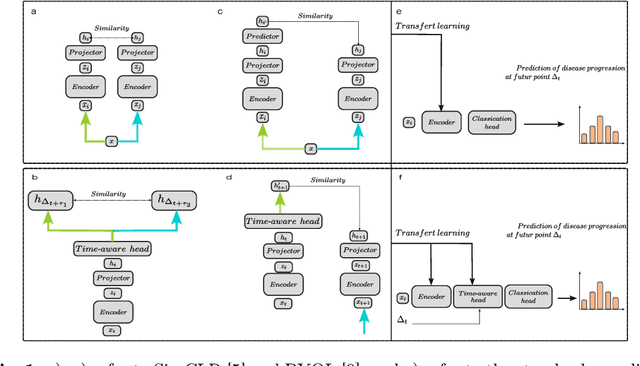
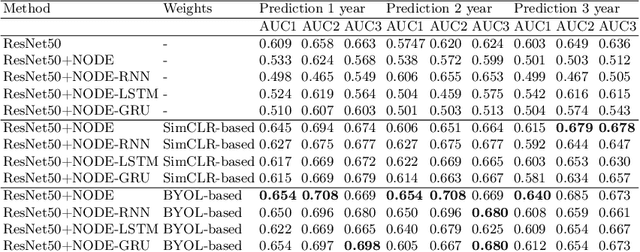
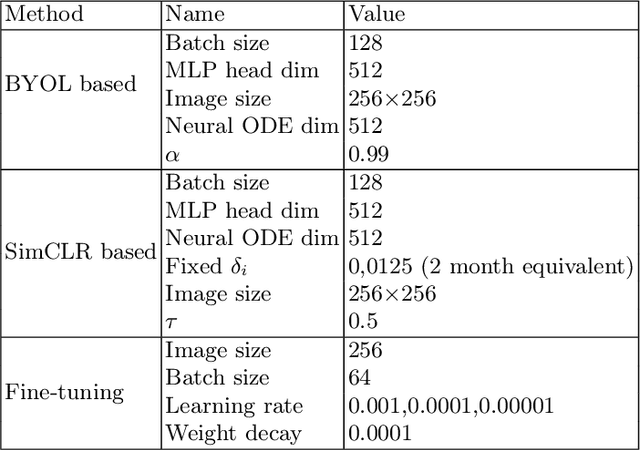
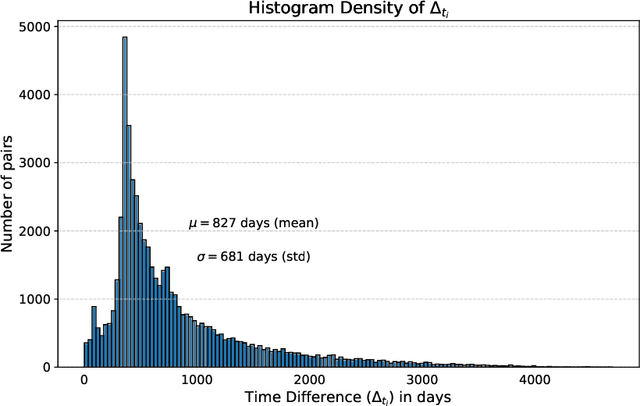
This work proposes a novel framework for analyzing disease progression using time-aware neural ordinary differential equations (NODE). We introduce a "time-aware head" in a framework trained through self-supervised learning (SSL) to leverage temporal information in latent space for data augmentation. This approach effectively integrates NODEs with SSL, offering significant performance improvements compared to traditional methods that lack explicit temporal integration. We demonstrate the effectiveness of our strategy for diabetic retinopathy progression prediction using the OPHDIAT database. Compared to the baseline, all NODE architectures achieve statistically significant improvements in area under the ROC curve (AUC) and Kappa metrics, highlighting the efficacy of pre-training with SSL-inspired approaches. Additionally, our framework promotes stable training for NODEs, a commonly encountered challenge in time-aware modeling.

L-MAE: Longitudinal masked auto-encoder with time and severity-aware encoding for diabetic retinopathy progression prediction

Pre-training strategies based on self-supervised learning (SSL) have proven to be effective pretext tasks for many downstream tasks in computer vision. Due to the significant disparity between medical and natural images, the application of typical SSL is not straightforward in medical imaging. Additionally, those pretext tasks often lack context, which is critical for computer-aided clinical decision support. In this paper, we developed a longitudinal masked auto-encoder (MAE) based on the well-known Transformer-based MAE. In particular, we explored the importance of time-aware position embedding as well as disease progression-aware masking. Taking into account the time between examinations instead of just scheduling them offers the benefit of capturing temporal changes and trends. The masking strategy, for its part, evolves during follow-up to better capture pathological changes, ensuring a more accurate assessment of disease progression. Using OPHDIAT, a large follow-up screening dataset targeting diabetic retinopathy (DR), we evaluated the pre-trained weights on a longitudinal task, which is to predict the severity label of the next visit within 3 years based on the past time series examinations. Our results demonstrated the relevancy of both time-aware position embedding and masking strategies based on disease progression knowledge. Compared to popular baseline models and standard longitudinal Transformers, these simple yet effective extensions significantly enhance the predictive ability of deep classification models.

Composable Core-sets for Determinant Maximization: A Simple Near-Optimal Algorithm

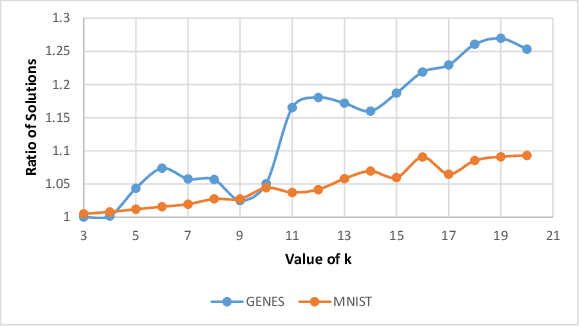
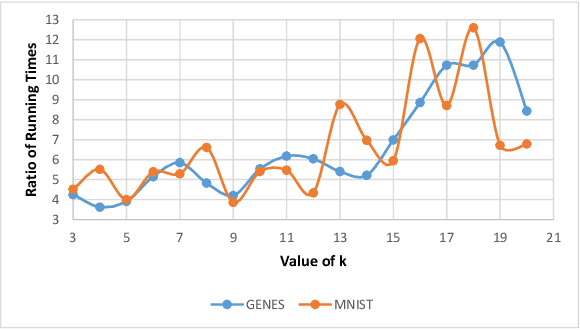
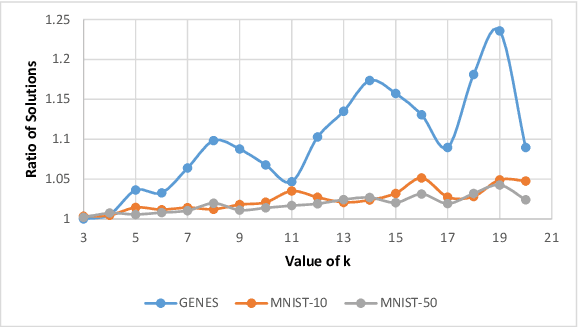
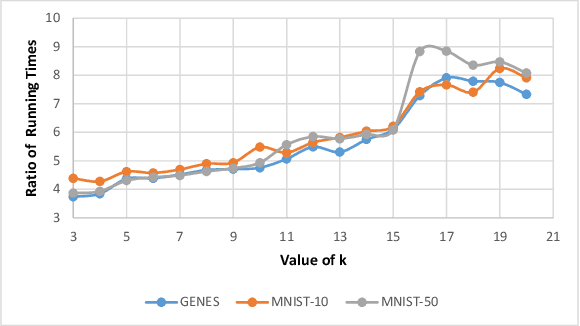
``Composable core-sets'' are an efficient framework for solving optimization problems in massive data models. In this work, we consider efficient construction of composable core-sets for the determinant maximization problem. This can also be cast as the MAP inference task for determinantal point processes, that have recently gained a lot of interest for modeling diversity and fairness. The problem was recently studied in [IMOR'18], where they designed composable core-sets with the optimal approximation bound of $\tilde O(k)^k$. On the other hand, the more practical Greedy algorithm has been previously used in similar contexts. In this work, first we provide a theoretical approximation guarantee of $O(C^{k^2})$ for the Greedy algorithm in the context of composable core-sets; Further, we propose to use a Local Search based algorithm that while being still practical, achieves a nearly optimal approximation bound of $O(k)^{2k}$; Finally, we implement all three algorithms and show the effectiveness of our proposed algorithm on standard data sets.

A Polynomial Time MCMC Method for Sampling from Continuous DPPs

We study the Gibbs sampling algorithm for continuous determinantal point processes. We show that, given a warm start, the Gibbs sampler generates a random sample from a continuous $k$-DPP defined on a $d$-dimensional domain by only taking $\text{poly}(k)$ number of steps. As an application, we design an algorithm to generate random samples from $k$-DPPs defined by a spherical Gaussian kernel on a unit sphere in $d$-dimensions, $\mathbb{S}^{d-1}$ in time polynomial in $k,d$.

Composable Core-sets for Determinant Maximization Problems via Spectral Spanners

We study a spectral generalization of classical combinatorial graph spanners to the spectral setting. Given a set of vectors $V\subseteq \Re^d$, we say a set $U\subseteq V$ is an $\alpha$-spectral spanner if for all $v\in V$ there is a probability distribution $\mu_v$ supported on $U$ such that $$vv^\intercal \preceq \alpha\cdot\mathbb{E}_{u\sim\mu_v} uu^\intercal.$$ We show that any set $V$ has an $\tilde{O}(d)$-spectral spanner of size $\tilde{O}(d)$ and this bound is almost optimal in the worst case. We use spectral spanners to study composable core-sets for spectral problems. We show that for many objective functions one can use a spectral spanner, independent of the underlying functions, as a core-set and obtain almost optimal composable core-sets. For example, for the determinant maximization problem we obtain an $\tilde{O}(k)^k$-composable core-set and we show that this is almost optimal in the worst case. Our algorithm is a spectral analogue of the classical greedy algorithm for finding (combinatorial) spanners in graphs. We expect that our spanners find many other applications in distributed or parallel models of computation. Our proof is spectral. As a side result of our techniques, we show that the rank of diagonally dominant lower-triangular matrices are robust under `small perturbations' which could be of independent interests.

Monte Carlo Markov Chain Algorithms for Sampling Strongly Rayleigh Distributions and Determinantal Point Processes

Strongly Rayleigh distributions are natural generalizations of product and determinantal probability distributions and satisfy strongest form of negative dependence properties. We show that the "natural" Monte Carlo Markov Chain (MCMC) is rapidly mixing in the support of a {\em homogeneous} strongly Rayleigh distribution. As a byproduct, our proof implies Markov chains can be used to efficiently generate approximate samples of a $k$-determinantal point process. This answers an open question raised by Deshpande and Rademacher.