Experimental Design Using Interlacing Polynomials

We present a unified deterministic approach for experimental design problems using the method of interlacing polynomials. Our framework recovers the best-known approximation guarantees for the well-studied D/A/E-design problems with simple analysis. Furthermore, we obtain improved non-trivial approximation guarantee for E-design in the challenging small budget regime. Additionally, our approach provides an optimal approximation guarantee for a generalized ratio objective that generalizes both D-design and A-design.

Fast Algorithms for Directed Graph Partitioning Using Flows and Reweighted Eigenvalues

We consider a new semidefinite programming relaxation for directed edge expansion, which is obtained by adding triangle inequalities to the reweighted eigenvalue formulation. Applying the matrix multiplicative weight update method to this relaxation, we derive almost linear-time algorithms to achieve $O(\sqrt{\log{n}})$-approximation and Cheeger-type guarantee for directed edge expansion, as well as an improved cut-matching game for directed graphs. This provides a primal-dual flow-based framework to obtain the best known algorithms for directed graph partitioning. The same approach also works for vertex expansion and for hypergraphs, providing a simple and unified approach to achieve the best known results for different expansion problems and different algorithmic techniques.

Experimental Design for Any $p$-Norm

We consider a general $p$-norm objective for experimental design problems that captures some well-studied objectives (D/A/E-design) as special cases. We prove that a randomized local search approach provides a unified algorithm to solve this problem for all $p$. This provides the first approximation algorithm for the general $p$-norm objective, and a nice interpolation of the best known bounds of the special cases.

Cheeger Inequalities for Directed Graphs and Hypergraphs Using Reweighted Eigenvalues

We derive Cheeger inequalities for directed graphs and hypergraphs using the reweighted eigenvalue approach that was recently developed for vertex expansion in undirected graphs [OZ22,KLT22,JPV22]. The goal is to develop a new spectral theory for directed graphs and an alternative spectral theory for hypergraphs. The first main result is a Cheeger inequality relating the vertex expansion $\vec{\psi}(G)$ of a directed graph $G$ to the vertex-capacitated maximum reweighted second eigenvalue $\vec{\lambda}_2^{v*}$: \[ \vec{\lambda}_2^{v*} \lesssim \vec{\psi}(G) \lesssim \sqrt{\vec{\lambda}_2^{v*} \cdot \log (\Delta/\vec{\lambda}_2^{v*})}. \] This provides a combinatorial characterization of the fastest mixing time of a directed graph by vertex expansion, and builds a new connection between reweighted eigenvalued, vertex expansion, and fastest mixing time for directed graphs. The second main result is a stronger Cheeger inequality relating the edge conductance $\vec{\phi}(G)$ of a directed graph $G$ to the edge-capacitated maximum reweighted second eigenvalue $\vec{\lambda}_2^{e*}$: \[ \vec{\lambda}_2^{e*} \lesssim \vec{\phi}(G) \lesssim \sqrt{\vec{\lambda}_2^{e*} \cdot \log (1/\vec{\lambda}_2^{e*})}. \] This provides a certificate for a directed graph to be an expander and a spectral algorithm to find a sparse cut in a directed graph, playing a similar role as Cheeger's inequality in certifying graph expansion and in the spectral partitioning algorithm for undirected graphs. We also use this reweighted eigenvalue approach to derive the improved Cheeger inequality for directed graphs, and furthermore to derive several Cheeger inequalities for hypergraphs that match and improve the existing results in [Lou15,CLTZ18]. These are supporting results that this provides a unifying approach to lift the spectral theory for undirected graphs to more general settings.

A Local Search Framework for Experimental Design

We present a local search framework to design and analyze both combinatorial algorithms and rounding algorithms for experimental design problems. This framework provides a unifying approach to match and improve all known results in D/A/E-design and to obtain new results in previously unknown settings. For combinatorial algorithms, we provide a new analysis of the classical Fedorov's exchange method. We prove that this simple local search algorithm works well as long as there exists an almost optimal solution with good condition number. Moreover, we design a new combinatorial local search algorithm for E-design using the regret minimization framework. For rounding algorithms, we provide a unified randomized exchange algorithm to match and improve previous results for D/A/E-design. Furthermore, the algorithm works in the more general setting to approximately satisfy multiple knapsack constraints, which can be used for weighted experimental design and for incorporating fairness constraints into experimental design.

Improved Cheeger's Inequality: Analysis of Spectral Partitioning Algorithms through Higher Order Spectral Gap

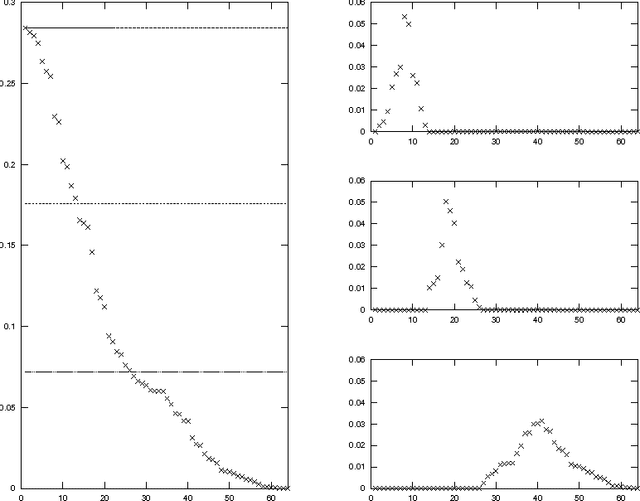
Let \phi(G) be the minimum conductance of an undirected graph G, and let 0=\lambda_1 <= \lambda_2 <=... <= \lambda_n <= 2 be the eigenvalues of the normalized Laplacian matrix of G. We prove that for any graph G and any k >= 2, \phi(G) = O(k) \lambda_2 / \sqrt{\lambda_k}, and this performance guarantee is achieved by the spectral partitioning algorithm. This improves Cheeger's inequality, and the bound is optimal up to a constant factor for any k. Our result shows that the spectral partitioning algorithm is a constant factor approximation algorithm for finding a sparse cut if \lambda_k$ is a constant for some constant k. This provides some theoretical justification to its empirical performance in image segmentation and clustering problems. We extend the analysis to other graph partitioning problems, including multi-way partition, balanced separator, and maximum cut.