Robust Graph Structure Learning with the Alignment of Features and Adjacency Matrix

To improve the robustness of graph neural networks (GNN), graph structure learning (GSL) has attracted great interest due to the pervasiveness of noise in graph data. Many approaches have been proposed for GSL to jointly learn a clean graph structure and corresponding representations. To extend the previous work, this paper proposes a novel regularized GSL approach, particularly with an alignment of feature information and graph information, which is motivated mainly by our derived lower bound of node-level Rademacher complexity for GNNs. Additionally, our proposed approach incorporates sparse dimensional reduction to leverage low-dimensional node features that are relevant to the graph structure. To evaluate the effectiveness of our approach, we conduct experiments on real-world graphs. The results demonstrate that our proposed GSL method outperforms several competitive baselines, especially in scenarios where the graph structures are heavily affected by noise. Overall, our research highlights the importance of integrating feature and graph information alignment in GSL, as inspired by our derived theoretical result, and showcases the superiority of our approach in handling noisy graph structures through comprehensive experiments on real-world datasets.

Personalized Federated Learning via Amortized Bayesian Meta-Learning

Federated learning is a decentralized and privacy-preserving technique that enables multiple clients to collaborate with a server to learn a global model without exposing their private data. However, the presence of statistical heterogeneity among clients poses a challenge, as the global model may struggle to perform well on each client's specific task. To address this issue, we introduce a new perspective on personalized federated learning through Amortized Bayesian Meta-Learning. Specifically, we propose a novel algorithm called \emph{FedABML}, which employs hierarchical variational inference across clients. The global prior aims to capture representations of common intrinsic structures from heterogeneous clients, which can then be transferred to their respective tasks and aid in the generation of accurate client-specific approximate posteriors through a few local updates. Our theoretical analysis provides an upper bound on the average generalization error and guarantees the generalization performance on unseen data. Finally, several empirical results are implemented to demonstrate that \emph{FedABML} outperforms several competitive baselines.

Stability and Generalization of $\ell_p$-Regularized Stochastic Learning for GCN

Graph convolutional networks (GCN) are viewed as one of the most popular representations among the variants of graph neural networks over graph data and have shown powerful performance in empirical experiments. That $\ell_2$-based graph smoothing enforces the global smoothness of GCN, while (soft) $\ell_1$-based sparse graph learning tends to promote signal sparsity to trade for discontinuity. This paper aims to quantify the trade-off of GCN between smoothness and sparsity, with the help of a general $\ell_p$-regularized $(1<p\leq 2)$ stochastic learning proposed within. While stability-based generalization analyses have been given in prior work for a second derivative objectiveness function, our $\ell_p$-regularized learning scheme does not satisfy such a smooth condition. To tackle this issue, we propose a novel SGD proximal algorithm for GCNs with an inexact operator. For a single-layer GCN, we establish an explicit theoretical understanding of GCN with the $\ell_p$-regularized stochastic learning by analyzing the stability of our SGD proximal algorithm. We conduct multiple empirical experiments to validate our theoretical findings.

SStaGCN: Simplified stacking based graph convolutional networks

Graph convolutional network (GCN) is a powerful model studied broadly in various graph structural data learning tasks. However, to mitigate the over-smoothing phenomenon, and deal with heterogeneous graph structural data, the design of GCN model remains a crucial issue to be investigated. In this paper, we propose a novel GCN called SStaGCN (Simplified stacking based GCN) by utilizing the ideas of stacking and aggregation, which is an adaptive general framework for tackling heterogeneous graph data. Specifically, we first use the base models of stacking to extract the node features of a graph. Subsequently, aggregation methods such as mean, attention and voting techniques are employed to further enhance the ability of node features extraction. Thereafter, the node features are considered as inputs and fed into vanilla GCN model. Furthermore, theoretical generalization bound analysis of the proposed model is explicitly given. Extensive experiments on $3$ public citation networks and another $3$ heterogeneous tabular data demonstrate the effectiveness and efficiency of the proposed approach over state-of-the-art GCNs. Notably, the proposed SStaGCN can efficiently mitigate the over-smoothing problem of GCN.

Kernel-based estimation for partially functional linear model: Minimax rates and randomized sketches

This paper considers the partially functional linear model (PFLM) where all predictive features consist of a functional covariate and a high dimensional scalar vector. Over an infinite dimensional reproducing kernel Hilbert space, the proposed estimation for PFLM is a least square approach with two mixed regularizations of a function-norm and an $\ell_1$-norm. Our main task in this paper is to establish the minimax rates for PFLM under high dimensional setting, and the optimal minimax rates of estimation is established by using various techniques in empirical process theory for analyzing kernel classes. In addition, we propose an efficient numerical algorithm based on randomized sketches of the kernel matrix. Several numerical experiments are implemented to support our method and optimization strategy.

Communication-efficient Byzantine-robust distributed learning with statistical guarantee

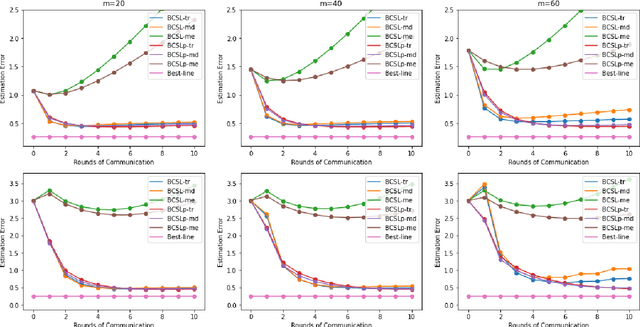
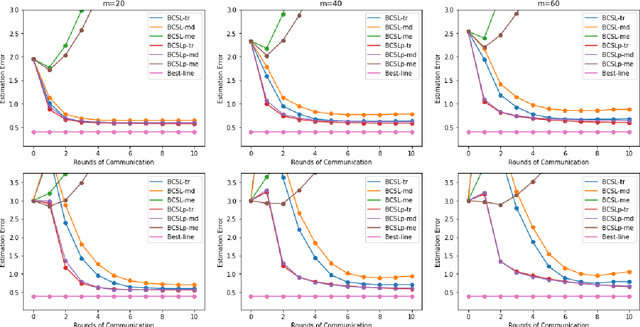
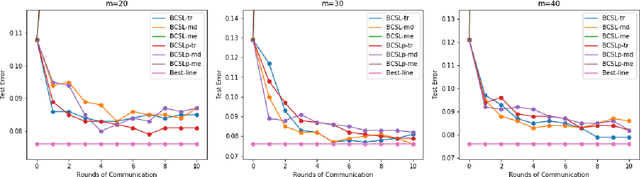
Communication efficiency and robustness are two major issues in modern distributed learning framework. This is due to the practical situations where some computing nodes may have limited communication power or may behave adversarial behaviors. To address the two issues simultaneously, this paper develops two communication-efficient and robust distributed learning algorithms for convex problems. Our motivation is based on surrogate likelihood framework and the median and trimmed mean operations. Particularly, the proposed algorithms are provably robust against Byzantine failures, and also achieve optimal statistical rates for strong convex losses and convex (non-smooth) penalties. For typical statistical models such as generalized linear models, our results show that statistical errors dominate optimization errors in finite iterations. Simulated and real data experiments are conducted to demonstrate the numerical performance of our algorithms.

Generalization bounds for graph convolutional neural networks via Rademacher complexity

This paper aims at studying the sample complexity of graph convolutional networks (GCNs), by providing tight upper bounds of Rademacher complexity for GCN models with a single hidden layer. Under regularity conditions, theses derived complexity bounds explicitly depend on the largest eigenvalue of graph convolution filter and the degree distribution of the graph. Again, we provide a lower bound of Rademacher complexity for GCNs to show optimality of our derived upper bounds. Taking two commonly used examples as representatives, we discuss the implications of our results in designing graph convolution filters an graph distribution.

Financial Market Directional Forecasting With Stacked Denoising Autoencoder

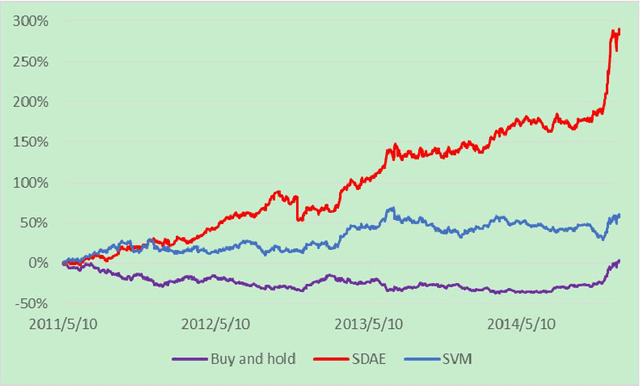
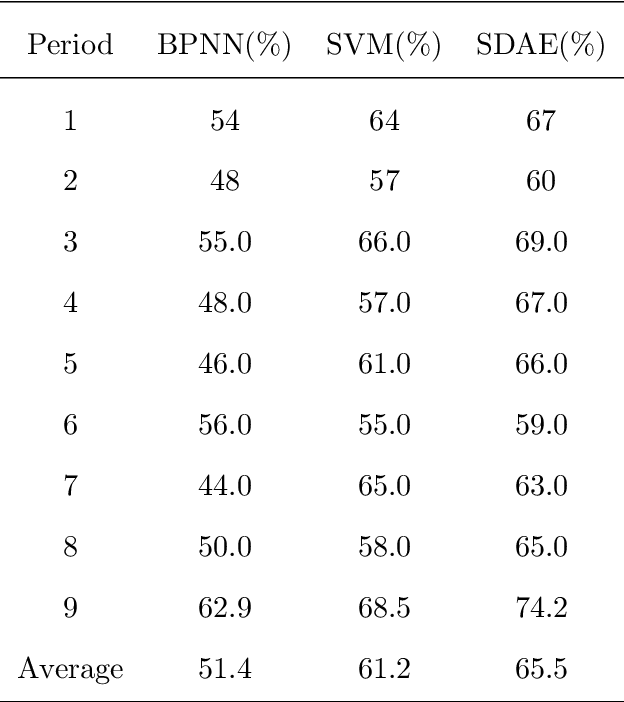
Forecasting stock market direction is always an amazing but challenging problem in finance. Although many popular shallow computational methods (such as Backpropagation Network and Support Vector Machine) have extensively been proposed, most algorithms have not yet attained a desirable level of applicability. In this paper, we present a deep learning model with strong ability to generate high level feature representations for accurate financial prediction. Precisely, a stacked denoising autoencoder (SDAE) from deep learning is applied to predict the daily CSI 300 index, from Shanghai and Shenzhen Stock Exchanges in China. We use six evaluation criteria to evaluate its performance compared with the back propagation network, support vector machine. The experiment shows that the underlying financial model with deep machine technology has a significant advantage for the prediction of the CSI 300 index.

Scalable kernel-based variable selection with sparsistency

Variable selection is central to high-dimensional data analysis, and various algorithms have been developed. Ideally, a variable selection algorithm shall be flexible, scalable, and with theoretical guarantee, yet most existing algorithms cannot attain these properties at the same time. In this article, a three-step variable selection algorithm is developed, involving kernel-based estimation of the regression function and its gradient functions as well as a hard thresholding. Its key advantage is that it assumes no explicit model assumption, admits general predictor effects, allows for scalable computation, and attains desirable asymptotic sparsistency. The proposed algorithm can be adapted to any reproducing kernel Hilbert space (RKHS) with different kernel functions, and can be extended to interaction selection with slight modification. Its computational cost is only linear in the data dimension, and can be further improved through parallel computing. The sparsistency of the proposed algorithm is established for general RKHS under mild conditions, including linear and Gaussian kernels as special cases. Its effectiveness is also supported by a variety of simulated and real examples.

A debiased distributed estimation for sparse partially linear models in diverging dimensions

We consider a distributed estimation of the double-penalized least squares approach for high dimensional partial linear models, where the sample with a total of $N$ data points is randomly distributed among $m$ machines and the parameters of interest are calculated by merging their $m$ individual estimators. This paper primarily focuses on the investigation of the high dimensional linear components in partial linear models, which is often of more interest. We propose a new debiased averaging estimator of parametric coefficients on the basis of each individual estimator, and establish new non-asymptotic oracle results in high dimensional and distributed settings, provided that $m\leq \sqrt{N/\log p}$ and other mild conditions are satisfied, where $p$ is the linear coefficient dimension. We also provide an experimental evaluation of the proposed method, indicating the numerical effectiveness on simulated data. Even under the classical non-distributed setting, we give the optimal rates of the parametric estimator with a looser tuning parameter limitation, which is required for our error analysis.