Panel semiparametric quantile regression neural network for electricity consumption forecasting

China has made great achievements in electric power industry during the long-term deepening of reform and opening up. However, the complex regional economic, social and natural conditions, electricity resources are not evenly distributed, which accounts for the electricity deficiency in some regions of China. It is desirable to develop a robust electricity forecasting model. Motivated by which, we propose a Panel Semiparametric Quantile Regression Neural Network (PSQRNN) by utilizing the artificial neural network and semiparametric quantile regression. The PSQRNN can explore a potential linear and nonlinear relationships among the variables, interpret the unobserved provincial heterogeneity, and maintain the interpretability of parametric models simultaneously. And the PSQRNN is trained by combining the penalized quantile regression with LASSO, ridge regression and backpropagation algorithm. To evaluate the prediction accuracy, an empirical analysis is conducted to analyze the provincial electricity consumption from 1999 to 2018 in China based on three scenarios. From which, one finds that the PSQRNN model performs better for electricity consumption forecasting by considering the economic and climatic factors. Finally, the provincial electricity consumptions of the next $5$ years (2019-2023) in China are reported by forecasting.

Communication-efficient Byzantine-robust distributed learning with statistical guarantee

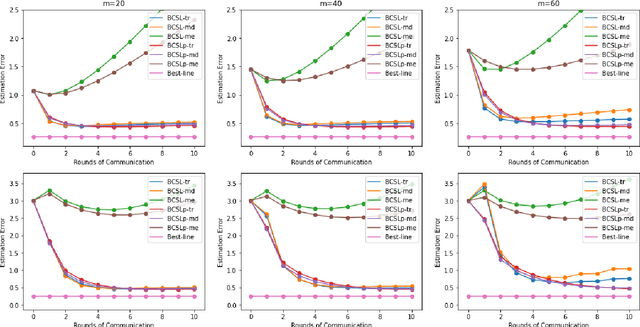
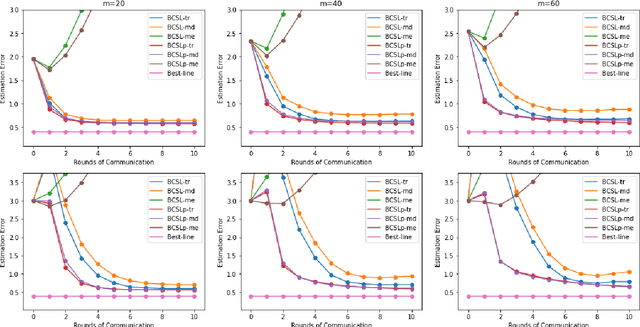
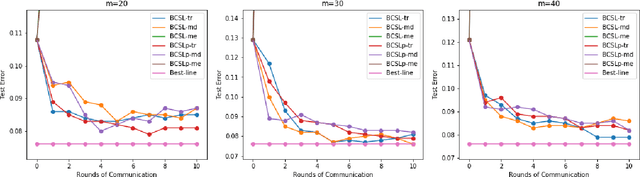
Communication efficiency and robustness are two major issues in modern distributed learning framework. This is due to the practical situations where some computing nodes may have limited communication power or may behave adversarial behaviors. To address the two issues simultaneously, this paper develops two communication-efficient and robust distributed learning algorithms for convex problems. Our motivation is based on surrogate likelihood framework and the median and trimmed mean operations. Particularly, the proposed algorithms are provably robust against Byzantine failures, and also achieve optimal statistical rates for strong convex losses and convex (non-smooth) penalties. For typical statistical models such as generalized linear models, our results show that statistical errors dominate optimization errors in finite iterations. Simulated and real data experiments are conducted to demonstrate the numerical performance of our algorithms.