A spatiotemporal deep learning framework for prediction of crack dynamics in heterogeneous solids: efficient mapping of concrete microstructures to its fracture properties

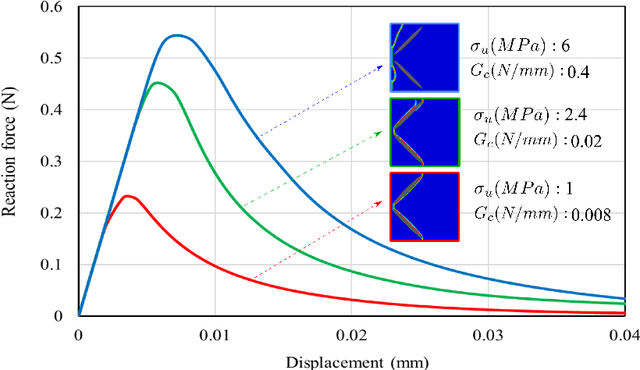
A spatiotemporal deep learning framework is proposed that is capable of 2D full-field prediction of fracture in concrete mesostructures. This framework not only predicts fractures but also captures the entire history of the fracture process, from the crack initiation in the interfacial transition zone to the subsequent propagation of the cracks in the mortar matrix. In addition, a convolutional neural network is developed which can predict the averaged stress-strain curve of the mesostructures. The UNet modeling framework, which comprises an encoder-decoder section with skip connections, is used as the deep learning surrogate model. Training and test data are generated from high-fidelity fracture simulations of randomly generated concrete mesostructures. These mesostructures include geometric variabilities such as different aggregate particle geometrical features, spatial distribution, and the total volume fraction of aggregates. The fracture simulations are carried out in Abaqus, utilizing the cohesive phase-field fracture modeling technique as the fracture modeling approach. In this work, to reduce the number of training datasets, the spatial distribution of three sets of material properties for three-phase concrete mesostructures, along with the spatial phase-field damage index, are fed to the UNet to predict the corresponding stress and spatial damage index at the subsequent step. It is shown that after the training process using this methodology, the UNet model is capable of accurately predicting damage on the unseen test dataset by using 470 datasets. Moreover, another novel aspect of this work is the conversion of irregular finite element data into regular grids using a developed pipeline. This approach allows for the implementation of less complex UNet architecture and facilitates the integration of phase-field fracture equations into surrogate models for future developments.

Finite Operator Learning: Bridging Neural Operators and Numerical Methods for Efficient Parametric Solution and Optimization of PDEs

We introduce a method that combines neural operators, physics-informed machine learning, and standard numerical methods for solving PDEs. The proposed approach extends each of the aforementioned methods and unifies them within a single framework. We can parametrically solve partial differential equations in a data-free manner and provide accurate sensitivities, meaning the derivatives of the solution space with respect to the design space. These capabilities enable gradient-based optimization without the typical sensitivity analysis costs, unlike adjoint methods that scale directly with the number of response functions. Our Finite Operator Learning (FOL) approach uses an uncomplicated feed-forward neural network model to directly map the discrete design space (i.e. parametric input space) to the discrete solution space (i.e. finite number of sensor points in the arbitrary shape domain) ensuring compliance with physical laws by designing them into loss functions. The discretized governing equations, as well as the design and solution spaces, can be derived from any well-established numerical techniques. In this work, we employ the Finite Element Method (FEM) to approximate fields and their spatial derivatives. Subsequently, we conduct Sobolev training to minimize a multi-objective loss function, which includes the discretized weak form of the energy functional, boundary conditions violations, and the stationarity of the residuals with respect to the design variables. Our study focuses on the steady-state heat equation within heterogeneous materials that exhibits significant phase contrast and possibly temperature-dependent conductivity. The network's tangent matrix is directly used for gradient-based optimization to improve the microstructure's heat transfer characteristics. ...

A finite element-based physics-informed operator learning framework for spatiotemporal partial differential equations on arbitrary domains

We propose a novel finite element-based physics-informed operator learning framework that allows for predicting spatiotemporal dynamics governed by partial differential equations (PDEs). The proposed framework employs a loss function inspired by the finite element method (FEM) with the implicit Euler time integration scheme. A transient thermal conduction problem is considered to benchmark the performance. The proposed operator learning framework takes a temperature field at the current time step as input and predicts a temperature field at the next time step. The Galerkin discretized weak formulation of the heat equation is employed to incorporate physics into the loss function, which is coined finite operator learning (FOL). Upon training, the networks successfully predict the temperature evolution over time for any initial temperature field at high accuracy compared to the FEM solution. The framework is also confirmed to be applicable to a heterogeneous thermal conductivity and arbitrary geometry. The advantages of FOL can be summarized as follows: First, the training is performed in an unsupervised manner, avoiding the need for a large data set prepared from costly simulations or experiments. Instead, random temperature patterns generated by the Gaussian random process and the Fourier series, combined with constant temperature fields, are used as training data to cover possible temperature cases. Second, shape functions and backward difference approximation are exploited for the domain discretization, resulting in a purely algebraic equation. This enhances training efficiency, as one avoids time-consuming automatic differentiation when optimizing weights and biases while accepting possible discretization errors. Finally, thanks to the interpolation power of FEM, any arbitrary geometry can be handled with FOL, which is crucial to addressing various engineering application scenarios.

Introducing a microstructure-embedded autoencoder approach for reconstructing high-resolution solution field data from a reduced parametric space

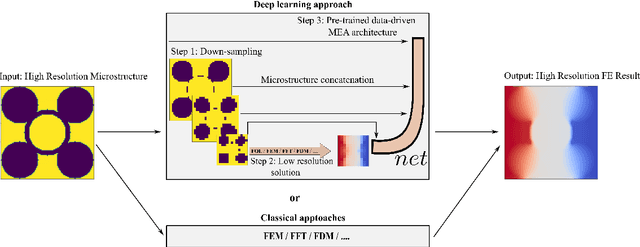
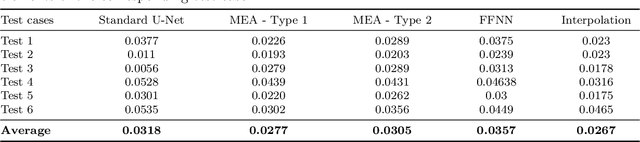
In this study, we develop a novel multi-fidelity deep learning approach that transforms low-fidelity solution maps into high-fidelity ones by incorporating parametric space information into a standard autoencoder architecture. This method's integration of parametric space information significantly reduces the need for training data to effectively predict high-fidelity solutions from low-fidelity ones. In this study, we examine a two-dimensional steady-state heat transfer analysis within a highly heterogeneous materials microstructure. The heat conductivity coefficients for two different materials are condensed from a 101 x 101 grid to smaller grids. We then solve the boundary value problem on the coarsest grid using a pre-trained physics-informed neural operator network known as Finite Operator Learning (FOL). The resulting low-fidelity solution is subsequently upscaled back to a 101 x 101 grid using a newly designed enhanced autoencoder. The novelty of the developed enhanced autoencoder lies in the concatenation of heat conductivity maps of different resolutions to the decoder segment in distinct steps. Hence the developed algorithm is named microstructure-embedded autoencoder (MEA). We compare the MEA outcomes with those from finite element methods, the standard U-Net, and various other upscaling techniques, including interpolation functions and feedforward neural networks (FFNN). Our analysis shows that MEA outperforms these methods in terms of computational efficiency and error on test cases. As a result, the MEA serves as a potential supplement to neural operator networks, effectively upscaling low-fidelity solutions to high fidelity while preserving critical details often lost in traditional upscaling methods, particularly at sharp interfaces like those seen with interpolation.

A finite operator learning technique for mapping the elastic properties of microstructures to their mechanical deformations

To develop faster solvers for governing physical equations in solid mechanics, we introduce a method that parametrically learns the solution to mechanical equilibrium. The introduced method outperforms traditional ones in terms of computational cost while acceptably maintaining accuracy. Moreover, it generalizes and enhances the standard physics-informed neural networks to learn a parametric solution with rather sharp discontinuities. We focus on micromechanics as an example, where the knowledge of the micro-mechanical solution, i.e., deformation and stress fields for a given heterogeneous microstructure, is crucial. The parameter under investigation is the Young modulus distribution within the heterogeneous solid system. Our method, inspired by operator learning and the finite element method, demonstrates the ability to train without relying on data from other numerical solvers. Instead, we leverage ideas from the finite element approach to efficiently set up loss functions algebraically, particularly based on the discretized weak form of the governing equations. Notably, our investigations reveal that physics-based training yields higher accuracy compared to purely data-driven approaches for unseen microstructures. In essence, this method achieves independence from data and enhances accuracy for predictions beyond the training range. The aforementioned observations apply here to heterogeneous elastic microstructures. Comparisons are also made with other well-known operator learning algorithms, such as DeepOnet, to further emphasize the advantages of the newly proposed architecture.

Integration of physics-informed operator learning and finite element method for parametric learning of partial differential equations

We present a method that employs physics-informed deep learning techniques for parametrically solving partial differential equations. The focus is on the steady-state heat equations within heterogeneous solids exhibiting significant phase contrast. Similar equations manifest in diverse applications like chemical diffusion, electrostatics, and Darcy flow. The neural network aims to establish the link between the complex thermal conductivity profiles and temperature distributions, as well as heat flux components within the microstructure, under fixed boundary conditions. A distinctive aspect is our independence from classical solvers like finite element methods for data. A noteworthy contribution lies in our novel approach to defining the loss function, based on the discretized weak form of the governing equation. This not only reduces the required order of derivatives but also eliminates the need for automatic differentiation in the construction of loss terms, accepting potential numerical errors from the chosen discretization method. As a result, the loss function in this work is an algebraic equation that significantly enhances training efficiency. We benchmark our methodology against the standard finite element method, demonstrating accurate yet faster predictions using the trained neural network for temperature and flux profiles. We also show higher accuracy by using the proposed method compared to purely data-driven approaches for unforeseen scenarios.

Learning solution of nonlinear constitutive material models using physics-informed neural networks: COMM-PINN

We applied physics-informed neural networks to solve the constitutive relations for nonlinear, path-dependent material behavior. As a result, the trained network not only satisfies all thermodynamic constraints but also instantly provides information about the current material state (i.e., free energy, stress, and the evolution of internal variables) under any given loading scenario without requiring initial data. One advantage of this work is that it bypasses the repetitive Newton iterations needed to solve nonlinear equations in complex material models. Additionally, strategies are provided to reduce the required order of derivation for obtaining the tangent operator. The trained model can be directly used in any finite element package (or other numerical methods) as a user-defined material model. However, challenges remain in the proper definition of collocation points and in integrating several non-equality constraints that become active or non-active simultaneously. We tested this methodology on rate-independent processes such as the classical von Mises plasticity model with a nonlinear hardening law, as well as local damage models for interface cracking behavior with a nonlinear softening law. Finally, we discuss the potential and remaining challenges for future developments of this new approach.

Mixed formulation of physics-informed neural networks for thermo-mechanically coupled systems and heterogeneous domains

Deep learning methods find a solution to a boundary value problem by defining loss functions of neural networks based on governing equations, boundary conditions, and initial conditions. Furthermore, the authors show that when it comes to many engineering problems, designing the loss functions based on first-order derivatives results in much better accuracy, especially when there is heterogeneity and variable jumps in the domain \cite{REZAEI2022PINN}. The so-called mixed formulation for PINN is applied to basic engineering problems such as the balance of linear momentum and diffusion problems. In this work, the proposed mixed formulation is further extended to solve multi-physical problems. In particular, we focus on a stationary thermo-mechanically coupled system of equations that can be utilized in designing the microstructure of advanced materials. First, sequential unsupervised training, and second, fully coupled unsupervised learning are discussed. The results of each approach are compared in terms of accuracy and corresponding computational cost. Finally, the idea of transfer learning is employed by combining data and physics to address the capability of the network to predict the response of the system for unseen cases. The outcome of this work will be useful for many other engineering applications where DL is employed on multiple coupled systems of equations.

AI enhanced finite element multiscale modelling and structural uncertainty analysis of a functionally graded porous beam

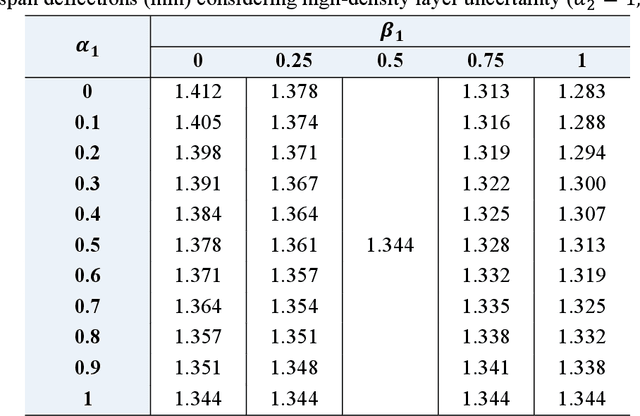
The local geometrical randomness of metal foams brings complexities to the performance prediction of porous structures. Although the relative density is commonly deemed as the key factor, the stochasticity of internal cell sizes and shapes has an apparent effect on the porous structural behaviour but the corresponding measurement is challenging. To address this issue, we are aimed to develop an assessment strategy for efficiently examining the foam properties by combining multiscale modelling and deep learning. The multiscale modelling is based on the finite element (FE) simulation employing representative volume elements (RVEs) with random cellular morphologies, mimicking the typical features of closed-cell Aluminium foams. A deep learning database is constructed for training the designed convolutional neural networks (CNNs) to establish a direct link between the mesoscopic porosity characteristics and the effective Youngs modulus of foams. The error range of CNN models leads to an uncertain mechanical performance, which is further evaluated in a structural uncertainty analysis on the FG porous three-layer beam consisting of two thin high-density layers and a thick low-density one, where the imprecise CNN predicted moduli are represented as triangular fuzzy numbers in double parametric form. The uncertain beam bending deflections under a mid-span point load are calculated with the aid of Timoshenko beam theory and the Ritz method. Our findings suggest the success in training CNN models to estimate RVE modulus using images with an average error of 5.92%. The evaluation of FG porous structures can be significantly simplified with the proposed method and connects to the mesoscopic cellular morphologies without establishing the mechanics model for local foams.

A mixed formulation for physics-informed neural networks as a potential solver for engineering problems in heterogeneous domains: comparison with finite element method

Physics-informed neural networks (PINNs) are capable of finding the solution for a given boundary value problem. We employ several ideas from the finite element method (FEM) to enhance the performance of existing PINNs in engineering problems. The main contribution of the current work is to promote using the spatial gradient of the primary variable as an output from separated neural networks. Later on, the strong form which has a higher order of derivatives is applied to the spatial gradients of the primary variable as the physical constraint. In addition, the so-called energy form of the problem is applied to the primary variable as an additional constraint for training. The proposed approach only required up to first-order derivatives to construct the physical loss functions. We discuss why this point is beneficial through various comparisons between different models. The mixed formulation-based PINNs and FE methods share some similarities. While the former minimizes the PDE and its energy form at given collocation points utilizing a complex nonlinear interpolation through a neural network, the latter does the same at element nodes with the help of shape functions. We focus on heterogeneous solids to show the capability of deep learning for predicting the solution in a complex environment under different boundary conditions. The performance of the proposed PINN model is checked against the solution from FEM on two prototype problems: elasticity and the Poisson equation (steady-state diffusion problem). We concluded that by properly designing the network architecture in PINN, the deep learning model has the potential to solve the unknowns in a heterogeneous domain without any available initial data from other sources. Finally, discussions are provided on the combination of PINN and FEM for a fast and accurate design of composite materials in future developments.