Rasoul Najafi Koopas
A spatiotemporal deep learning framework for prediction of crack dynamics in heterogeneous solids: efficient mapping of concrete microstructures to its fracture properties
Jul 24, 2024

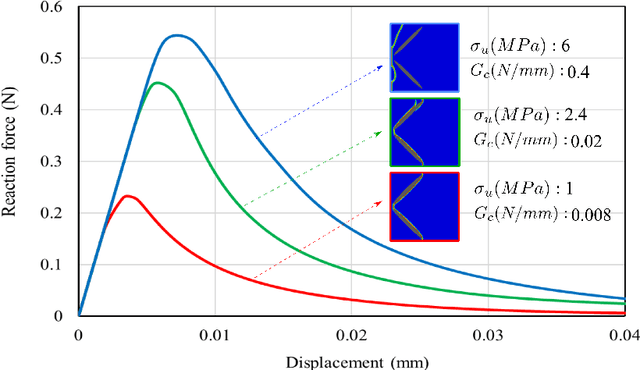

Abstract:A spatiotemporal deep learning framework is proposed that is capable of 2D full-field prediction of fracture in concrete mesostructures. This framework not only predicts fractures but also captures the entire history of the fracture process, from the crack initiation in the interfacial transition zone to the subsequent propagation of the cracks in the mortar matrix. In addition, a convolutional neural network is developed which can predict the averaged stress-strain curve of the mesostructures. The UNet modeling framework, which comprises an encoder-decoder section with skip connections, is used as the deep learning surrogate model. Training and test data are generated from high-fidelity fracture simulations of randomly generated concrete mesostructures. These mesostructures include geometric variabilities such as different aggregate particle geometrical features, spatial distribution, and the total volume fraction of aggregates. The fracture simulations are carried out in Abaqus, utilizing the cohesive phase-field fracture modeling technique as the fracture modeling approach. In this work, to reduce the number of training datasets, the spatial distribution of three sets of material properties for three-phase concrete mesostructures, along with the spatial phase-field damage index, are fed to the UNet to predict the corresponding stress and spatial damage index at the subsequent step. It is shown that after the training process using this methodology, the UNet model is capable of accurately predicting damage on the unseen test dataset by using 470 datasets. Moreover, another novel aspect of this work is the conversion of irregular finite element data into regular grids using a developed pipeline. This approach allows for the implementation of less complex UNet architecture and facilitates the integration of phase-field fracture equations into surrogate models for future developments.
Introducing a microstructure-embedded autoencoder approach for reconstructing high-resolution solution field data from a reduced parametric space
May 07, 2024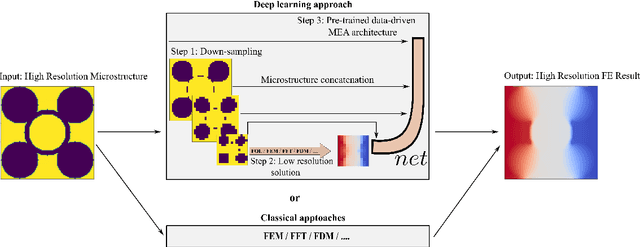


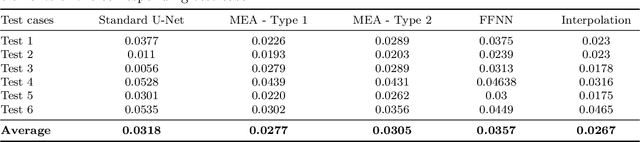
Abstract:In this study, we develop a novel multi-fidelity deep learning approach that transforms low-fidelity solution maps into high-fidelity ones by incorporating parametric space information into a standard autoencoder architecture. This method's integration of parametric space information significantly reduces the need for training data to effectively predict high-fidelity solutions from low-fidelity ones. In this study, we examine a two-dimensional steady-state heat transfer analysis within a highly heterogeneous materials microstructure. The heat conductivity coefficients for two different materials are condensed from a 101 x 101 grid to smaller grids. We then solve the boundary value problem on the coarsest grid using a pre-trained physics-informed neural operator network known as Finite Operator Learning (FOL). The resulting low-fidelity solution is subsequently upscaled back to a 101 x 101 grid using a newly designed enhanced autoencoder. The novelty of the developed enhanced autoencoder lies in the concatenation of heat conductivity maps of different resolutions to the decoder segment in distinct steps. Hence the developed algorithm is named microstructure-embedded autoencoder (MEA). We compare the MEA outcomes with those from finite element methods, the standard U-Net, and various other upscaling techniques, including interpolation functions and feedforward neural networks (FFNN). Our analysis shows that MEA outperforms these methods in terms of computational efficiency and error on test cases. As a result, the MEA serves as a potential supplement to neural operator networks, effectively upscaling low-fidelity solutions to high fidelity while preserving critical details often lost in traditional upscaling methods, particularly at sharp interfaces like those seen with interpolation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge