Finite Operator Learning: Bridging Neural Operators and Numerical Methods for Efficient Parametric Solution and Optimization of PDEs

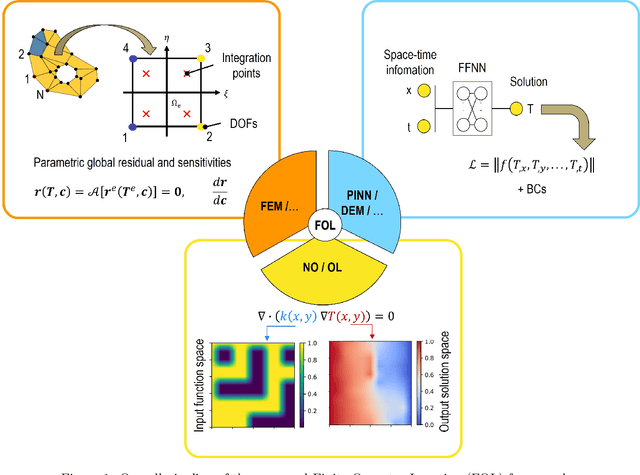
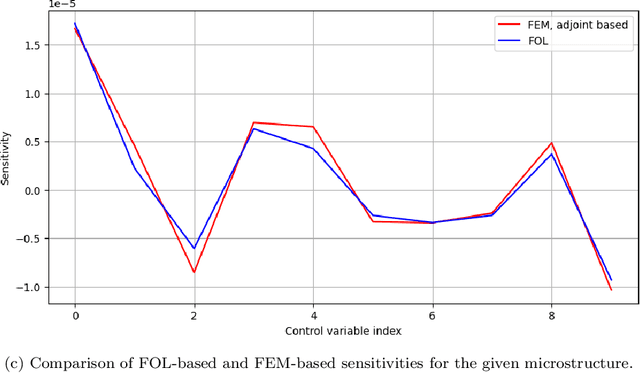
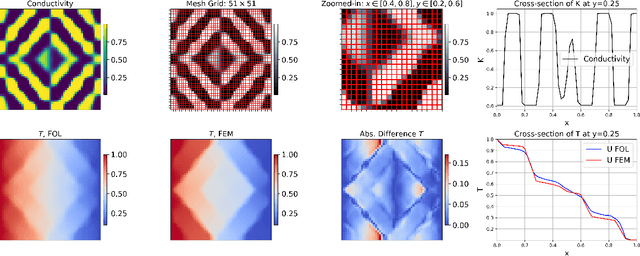
We introduce a method that combines neural operators, physics-informed machine learning, and standard numerical methods for solving PDEs. The proposed approach extends each of the aforementioned methods and unifies them within a single framework. We can parametrically solve partial differential equations in a data-free manner and provide accurate sensitivities, meaning the derivatives of the solution space with respect to the design space. These capabilities enable gradient-based optimization without the typical sensitivity analysis costs, unlike adjoint methods that scale directly with the number of response functions. Our Finite Operator Learning (FOL) approach uses an uncomplicated feed-forward neural network model to directly map the discrete design space (i.e. parametric input space) to the discrete solution space (i.e. finite number of sensor points in the arbitrary shape domain) ensuring compliance with physical laws by designing them into loss functions. The discretized governing equations, as well as the design and solution spaces, can be derived from any well-established numerical techniques. In this work, we employ the Finite Element Method (FEM) to approximate fields and their spatial derivatives. Subsequently, we conduct Sobolev training to minimize a multi-objective loss function, which includes the discretized weak form of the energy functional, boundary conditions violations, and the stationarity of the residuals with respect to the design variables. Our study focuses on the steady-state heat equation within heterogeneous materials that exhibits significant phase contrast and possibly temperature-dependent conductivity. The network's tangent matrix is directly used for gradient-based optimization to improve the microstructure's heat transfer characteristics. ...

A finite element-based physics-informed operator learning framework for spatiotemporal partial differential equations on arbitrary domains

We propose a novel finite element-based physics-informed operator learning framework that allows for predicting spatiotemporal dynamics governed by partial differential equations (PDEs). The proposed framework employs a loss function inspired by the finite element method (FEM) with the implicit Euler time integration scheme. A transient thermal conduction problem is considered to benchmark the performance. The proposed operator learning framework takes a temperature field at the current time step as input and predicts a temperature field at the next time step. The Galerkin discretized weak formulation of the heat equation is employed to incorporate physics into the loss function, which is coined finite operator learning (FOL). Upon training, the networks successfully predict the temperature evolution over time for any initial temperature field at high accuracy compared to the FEM solution. The framework is also confirmed to be applicable to a heterogeneous thermal conductivity and arbitrary geometry. The advantages of FOL can be summarized as follows: First, the training is performed in an unsupervised manner, avoiding the need for a large data set prepared from costly simulations or experiments. Instead, random temperature patterns generated by the Gaussian random process and the Fourier series, combined with constant temperature fields, are used as training data to cover possible temperature cases. Second, shape functions and backward difference approximation are exploited for the domain discretization, resulting in a purely algebraic equation. This enhances training efficiency, as one avoids time-consuming automatic differentiation when optimizing weights and biases while accepting possible discretization errors. Finally, thanks to the interpolation power of FEM, any arbitrary geometry can be handled with FOL, which is crucial to addressing various engineering application scenarios.

A finite operator learning technique for mapping the elastic properties of microstructures to their mechanical deformations

To develop faster solvers for governing physical equations in solid mechanics, we introduce a method that parametrically learns the solution to mechanical equilibrium. The introduced method outperforms traditional ones in terms of computational cost while acceptably maintaining accuracy. Moreover, it generalizes and enhances the standard physics-informed neural networks to learn a parametric solution with rather sharp discontinuities. We focus on micromechanics as an example, where the knowledge of the micro-mechanical solution, i.e., deformation and stress fields for a given heterogeneous microstructure, is crucial. The parameter under investigation is the Young modulus distribution within the heterogeneous solid system. Our method, inspired by operator learning and the finite element method, demonstrates the ability to train without relying on data from other numerical solvers. Instead, we leverage ideas from the finite element approach to efficiently set up loss functions algebraically, particularly based on the discretized weak form of the governing equations. Notably, our investigations reveal that physics-based training yields higher accuracy compared to purely data-driven approaches for unseen microstructures. In essence, this method achieves independence from data and enhances accuracy for predictions beyond the training range. The aforementioned observations apply here to heterogeneous elastic microstructures. Comparisons are also made with other well-known operator learning algorithms, such as DeepOnet, to further emphasize the advantages of the newly proposed architecture.

Integration of physics-informed operator learning and finite element method for parametric learning of partial differential equations

We present a method that employs physics-informed deep learning techniques for parametrically solving partial differential equations. The focus is on the steady-state heat equations within heterogeneous solids exhibiting significant phase contrast. Similar equations manifest in diverse applications like chemical diffusion, electrostatics, and Darcy flow. The neural network aims to establish the link between the complex thermal conductivity profiles and temperature distributions, as well as heat flux components within the microstructure, under fixed boundary conditions. A distinctive aspect is our independence from classical solvers like finite element methods for data. A noteworthy contribution lies in our novel approach to defining the loss function, based on the discretized weak form of the governing equation. This not only reduces the required order of derivatives but also eliminates the need for automatic differentiation in the construction of loss terms, accepting potential numerical errors from the chosen discretization method. As a result, the loss function in this work is an algebraic equation that significantly enhances training efficiency. We benchmark our methodology against the standard finite element method, demonstrating accurate yet faster predictions using the trained neural network for temperature and flux profiles. We also show higher accuracy by using the proposed method compared to purely data-driven approaches for unforeseen scenarios.