AI enhanced finite element multiscale modelling and structural uncertainty analysis of a functionally graded porous beam

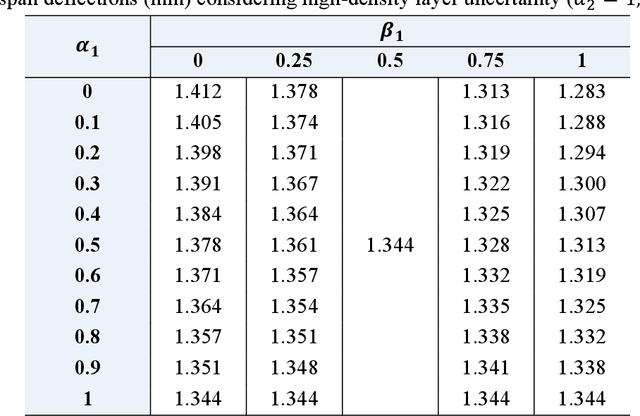
The local geometrical randomness of metal foams brings complexities to the performance prediction of porous structures. Although the relative density is commonly deemed as the key factor, the stochasticity of internal cell sizes and shapes has an apparent effect on the porous structural behaviour but the corresponding measurement is challenging. To address this issue, we are aimed to develop an assessment strategy for efficiently examining the foam properties by combining multiscale modelling and deep learning. The multiscale modelling is based on the finite element (FE) simulation employing representative volume elements (RVEs) with random cellular morphologies, mimicking the typical features of closed-cell Aluminium foams. A deep learning database is constructed for training the designed convolutional neural networks (CNNs) to establish a direct link between the mesoscopic porosity characteristics and the effective Youngs modulus of foams. The error range of CNN models leads to an uncertain mechanical performance, which is further evaluated in a structural uncertainty analysis on the FG porous three-layer beam consisting of two thin high-density layers and a thick low-density one, where the imprecise CNN predicted moduli are represented as triangular fuzzy numbers in double parametric form. The uncertain beam bending deflections under a mid-span point load are calculated with the aid of Timoshenko beam theory and the Ritz method. Our findings suggest the success in training CNN models to estimate RVE modulus using images with an average error of 5.92%. The evaluation of FG porous structures can be significantly simplified with the proposed method and connects to the mesoscopic cellular morphologies without establishing the mechanics model for local foams.

A mixed formulation for physics-informed neural networks as a potential solver for engineering problems in heterogeneous domains: comparison with finite element method

Physics-informed neural networks (PINNs) are capable of finding the solution for a given boundary value problem. We employ several ideas from the finite element method (FEM) to enhance the performance of existing PINNs in engineering problems. The main contribution of the current work is to promote using the spatial gradient of the primary variable as an output from separated neural networks. Later on, the strong form which has a higher order of derivatives is applied to the spatial gradients of the primary variable as the physical constraint. In addition, the so-called energy form of the problem is applied to the primary variable as an additional constraint for training. The proposed approach only required up to first-order derivatives to construct the physical loss functions. We discuss why this point is beneficial through various comparisons between different models. The mixed formulation-based PINNs and FE methods share some similarities. While the former minimizes the PDE and its energy form at given collocation points utilizing a complex nonlinear interpolation through a neural network, the latter does the same at element nodes with the help of shape functions. We focus on heterogeneous solids to show the capability of deep learning for predicting the solution in a complex environment under different boundary conditions. The performance of the proposed PINN model is checked against the solution from FEM on two prototype problems: elasticity and the Poisson equation (steady-state diffusion problem). We concluded that by properly designing the network architecture in PINN, the deep learning model has the potential to solve the unknowns in a heterogeneous domain without any available initial data from other sources. Finally, discussions are provided on the combination of PINN and FEM for a fast and accurate design of composite materials in future developments.

A deep learned nanowire segmentation model using synthetic data augmentation

Automatized object identification and feature analysis of experimental image data are indispensable for data-driven material science; deep-learning-based segmentation algorithms have been shown to be a promising technique to achieve this goal. However, acquiring high-resolution experimental images and assigning labels in order to train such algorithms is challenging and costly in terms of both time and labor. In the present work, we apply synthetic images, which resemble the experimental image data in terms of geometrical and visual features, to train state-of-art deep learning-based Mask R-CNN algorithms to segment vanadium pentoxide (V2O5) nanowires, a canonical cathode material, within optical intensity-based images from spectromicroscopy. The performance evaluation demonstrates that even though the deep learning model is trained on pure synthetically generated structures, it can segment real optical intensity-based spectromicroscopy images of complex V2O5 nanowire structures in overlapped particle networks, thus providing reliable statistical information. The model can further be used to segment nanowires in scanning electron microscopy (SEM) images, which are fundamentally different from the training dataset known to the model. The proposed methodology of using a purely synthetic dataset to train the deep learning model can be extended to any optical intensity-based images of variable particle morphology, extent of agglomeration, material class, and beyond.

Lossless Multi-Scale Constitutive Elastic Relations with Artificial Intelligence

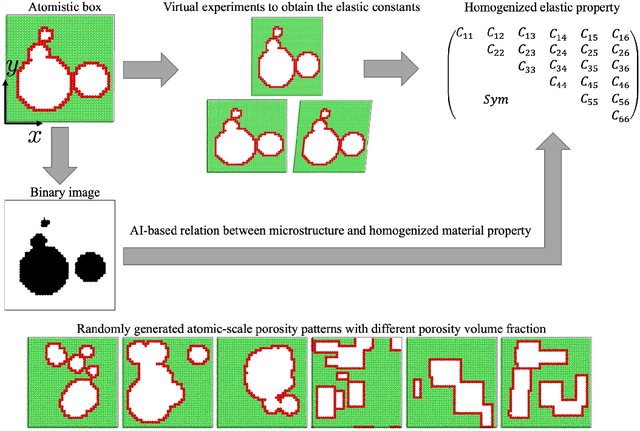
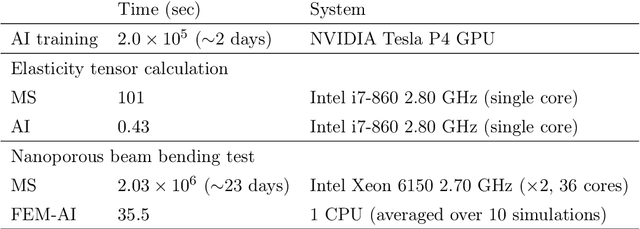
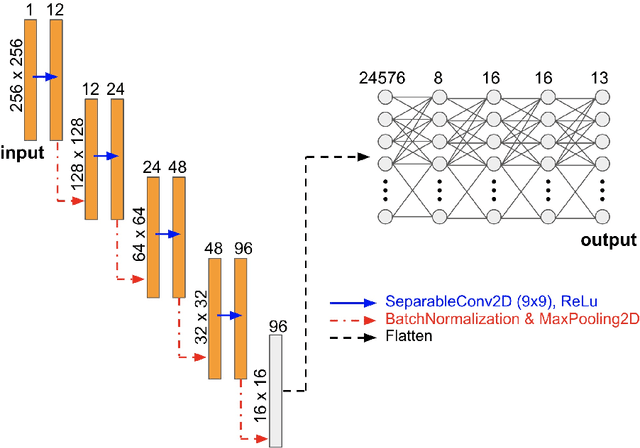
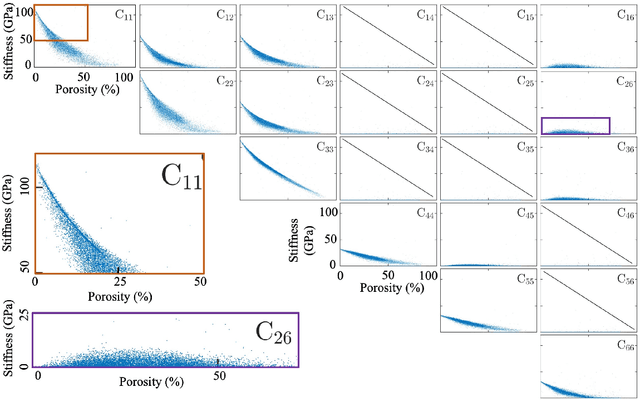
The elastic properties of materials derive from their electronic and atomic nature. However, simulating bulk materials fully at these scales is not feasible, so that typically homogenized continuum descriptions are used instead. A seamless and lossless transition of the constitutive description of the elastic response of materials between these two scales has been so far elusive. Here we show how this problem can be overcome by using Artificial Intelligence (AI). A Convolutional Neural Network (CNN) model is trained, by taking the structure image of a nanoporous material as input and the corresponding elasticity tensor, calculated from Molecular Statics (MS), as output. Trained with the atomistic data, the CNN model captures the size- and pore-dependency of the material's elastic properties which, on the physics side, can stem from surfaces and non-local effects. Such effects are often ignored in upscaling from atomistic to classical continuum theory. To demonstrate the accuracy and the efficiency of the trained CNN model, a Finite Element Method (FEM) based result of an elastically deformed nanoporous beam equipped with the CNN as constitutive law is compared with that by a full atomistic simulation. The good agreement between the atomistic simulations and the FEM-AI combination for a system with size and surface effects establishes a new lossless scale bridging approach to such problems. The trained CNN model deviates from the atomistic result by 9.6\% for porosity scenarios of up to 90\% but it is about 230 times faster than the MS calculation and does not require to change simulation methods between different scales. The efficiency of the CNN evaluation together with the preservation of important atomistic effects makes the trained model an effective atomistically-informed constitutive model for macroscopic simulations of nanoporous materials and solving of inverse problems.