Comparison of two artificial neural networks trained for the surrogate modeling of stress in materially heterogeneous elastoplastic solids

The purpose of this work is the systematic comparison of the application of two artificial neural networks (ANNs) to the surrogate modeling of the stress field in materially heterogeneous periodic polycrystalline microstructures. The first ANN is a UNet-based convolutional neural network (CNN) for periodic data, and the second is based on Fourier neural operators (FNO). Both of these were trained, validated, and tested with results from the numerical solution of the boundary-value problem (BVP) for quasi-static mechanical equilibrium in periodic grain microstructures with square domains. More specifically, these ANNs were trained to correlate the spatial distribution of material properties with the equilibrium stress field under uniaxial tensile loading. The resulting trained ANNs (tANNs) calculate the stress field for a given microstructure on the order of 1000 (UNet) to 2500 (FNO) times faster than the numerical solution of the corresponding BVP. For microstructures in the test dataset, the FNO-based tANN, or simply FNO, is more accurate than its UNet-based counterpart; the normalized mean absolute error of different stress components for the former is 0.25-0.40% as compared to 1.41-2.15% for the latter. Errors in FNO are restricted to grain boundary regions, whereas the error in U-Net also comes from within the grain. In comparison to U-Net, errors in FNO are more robust to large variations in spatial resolution as well as small variations in grain density. On other hand, errors in U-Net are robust to variations in boundary box aspect ratio, whereas errors in FNO increase as the domain becomes rectangular. Both tANNs are however unable to reproduce strong stress gradients, especially around regions of stress concentration.

Lossless Multi-Scale Constitutive Elastic Relations with Artificial Intelligence

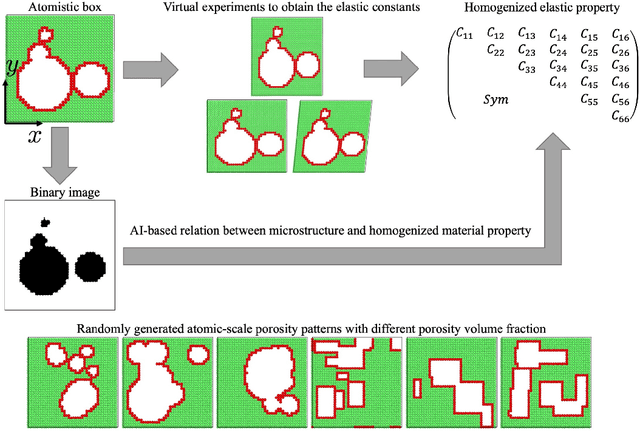
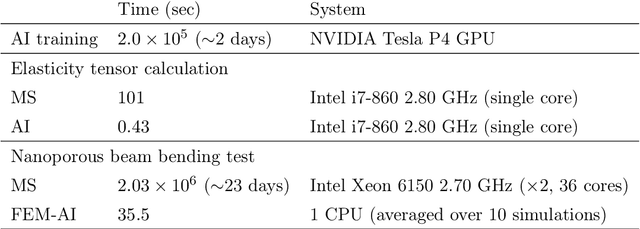
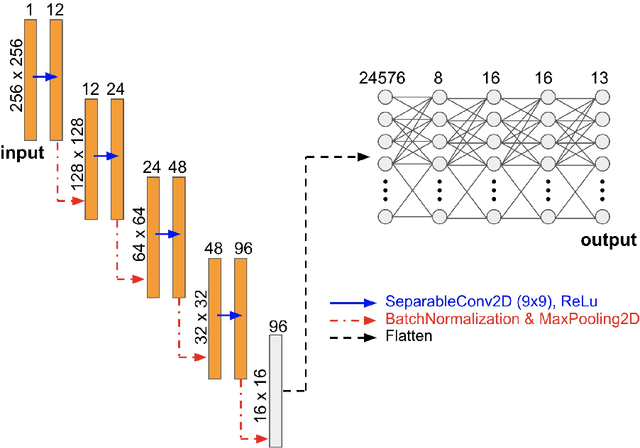
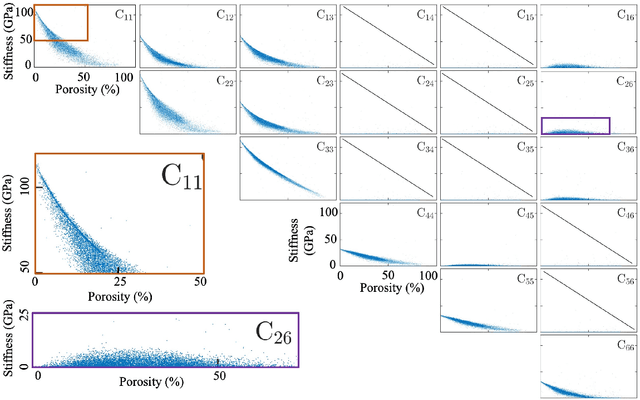
The elastic properties of materials derive from their electronic and atomic nature. However, simulating bulk materials fully at these scales is not feasible, so that typically homogenized continuum descriptions are used instead. A seamless and lossless transition of the constitutive description of the elastic response of materials between these two scales has been so far elusive. Here we show how this problem can be overcome by using Artificial Intelligence (AI). A Convolutional Neural Network (CNN) model is trained, by taking the structure image of a nanoporous material as input and the corresponding elasticity tensor, calculated from Molecular Statics (MS), as output. Trained with the atomistic data, the CNN model captures the size- and pore-dependency of the material's elastic properties which, on the physics side, can stem from surfaces and non-local effects. Such effects are often ignored in upscaling from atomistic to classical continuum theory. To demonstrate the accuracy and the efficiency of the trained CNN model, a Finite Element Method (FEM) based result of an elastically deformed nanoporous beam equipped with the CNN as constitutive law is compared with that by a full atomistic simulation. The good agreement between the atomistic simulations and the FEM-AI combination for a system with size and surface effects establishes a new lossless scale bridging approach to such problems. The trained CNN model deviates from the atomistic result by 9.6\% for porosity scenarios of up to 90\% but it is about 230 times faster than the MS calculation and does not require to change simulation methods between different scales. The efficiency of the CNN evaluation together with the preservation of important atomistic effects makes the trained model an effective atomistically-informed constitutive model for macroscopic simulations of nanoporous materials and solving of inverse problems.