Divergence-free neural operators for stress field modeling in polycrystalline materials

The purpose of the current work is the development and comparison of Fourier neural operators (FNOs) for surrogate modeling of the quasi-static mechanical response of polycrystalline materials. Three types of such FNOs are considered here: a physics-guided FNO (PgFNO), a physics-informed FNO (PiFNO), and a physics-encoded FNO (PeFNO). These are trained and compared with the help of stress field data from a reference model for heterogeneous elastic materials with a periodic grain microstructure. Whereas PgFNO training is based solely on these data, that of the PiFNO and PeFNO is in addition constrained by the requirement that stress fields satisfy mechanical equilibrium, i.e., be divergence-free. The difference between the PiFNO and PeFNO lies in how this constraint is taken into account; in the PiFNO, it is included in the loss function, whereas in the PeFNO, it is "encoded" in the operator architecture. In the current work, this encoding is based on a stress potential and Fourier transforms. As a result, only the training of the PiFNO is constrained by mechanical equilibrium; in contrast, mechanical equilibrium constrains both the training and output of the PeFNO. Due in particular to this, stress fields calculated by the trained PeFNO are significantly more accurate than those calculated by the trained PiFNO in the example cases considered.

Comparison of two artificial neural networks trained for the surrogate modeling of stress in materially heterogeneous elastoplastic solids

The purpose of this work is the systematic comparison of the application of two artificial neural networks (ANNs) to the surrogate modeling of the stress field in materially heterogeneous periodic polycrystalline microstructures. The first ANN is a UNet-based convolutional neural network (CNN) for periodic data, and the second is based on Fourier neural operators (FNO). Both of these were trained, validated, and tested with results from the numerical solution of the boundary-value problem (BVP) for quasi-static mechanical equilibrium in periodic grain microstructures with square domains. More specifically, these ANNs were trained to correlate the spatial distribution of material properties with the equilibrium stress field under uniaxial tensile loading. The resulting trained ANNs (tANNs) calculate the stress field for a given microstructure on the order of 1000 (UNet) to 2500 (FNO) times faster than the numerical solution of the corresponding BVP. For microstructures in the test dataset, the FNO-based tANN, or simply FNO, is more accurate than its UNet-based counterpart; the normalized mean absolute error of different stress components for the former is 0.25-0.40% as compared to 1.41-2.15% for the latter. Errors in FNO are restricted to grain boundary regions, whereas the error in U-Net also comes from within the grain. In comparison to U-Net, errors in FNO are more robust to large variations in spatial resolution as well as small variations in grain density. On other hand, errors in U-Net are robust to variations in boundary box aspect ratio, whereas errors in FNO increase as the domain becomes rectangular. Both tANNs are however unable to reproduce strong stress gradients, especially around regions of stress concentration.

Accelerating phase-field-based simulation via machine learning

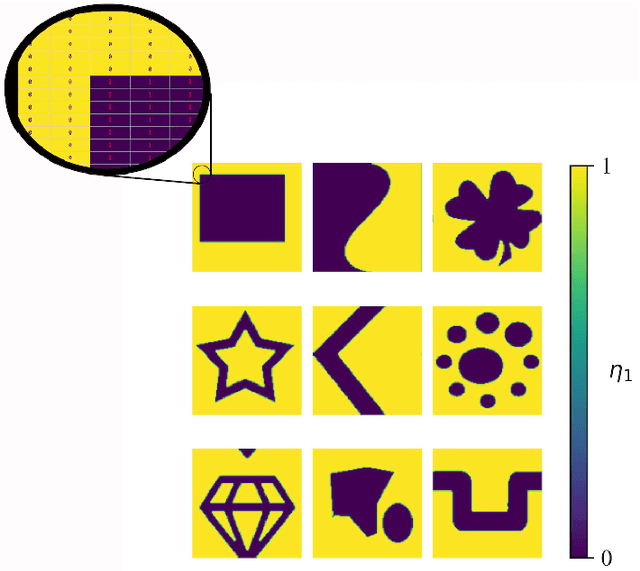
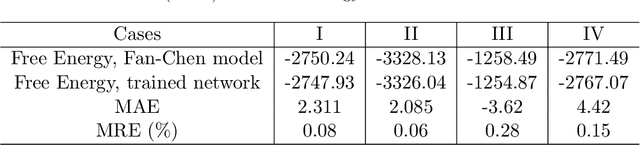
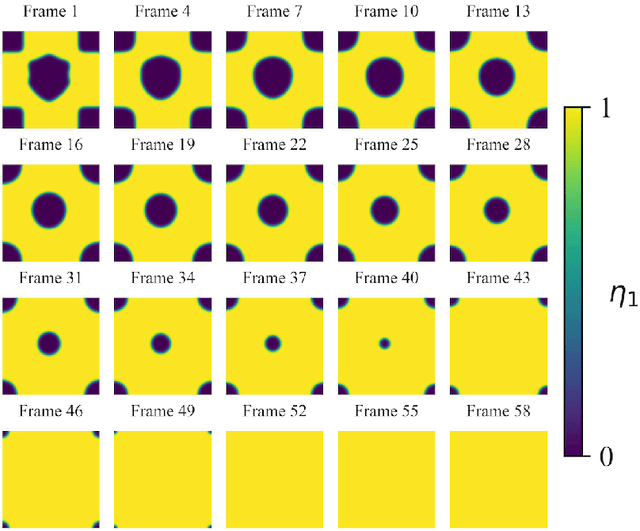
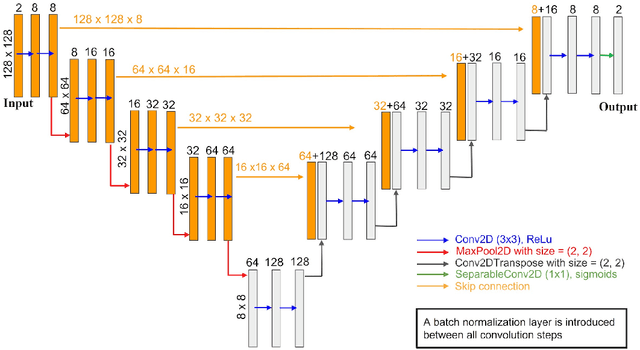
Phase-field-based models have become common in material science, mechanics, physics, biology, chemistry, and engineering for the simulation of microstructure evolution. Yet, they suffer from the drawback of being computationally very costly when applied to large, complex systems. To reduce such computational costs, a Unet-based artificial neural network is developed as a surrogate model in the current work. Training input for this network is obtained from the results of the numerical solution of initial-boundary-value problems (IBVPs) based on the Fan-Chen model for grain microstructure evolution. In particular, about 250 different simulations with varying initial order parameters are carried out and 200 frames of the time evolution of the phase fields are stored for each simulation. The network is trained with 90% of this data, taking the $i$-th frame of a simulation, i.e. order parameter field, as input, and producing the $(i+1)$-th frame as the output. Evaluation of the network is carried out with a test dataset consisting of 2200 microstructures based on different configurations than originally used for training. The trained network is applied recursively on initial order parameters to calculate the time evolution of the phase fields. The results are compared to the ones obtained from the conventional numerical solution in terms of the errors in order parameters and the system's free energy. The resulting order parameter error averaged over all points and all simulation cases is 0.005 and the relative error in the total free energy in all simulation boxes does not exceed 1%.