Reflections from the 2024 Large Language Model (LLM) Hackathon for Applications in Materials Science and Chemistry

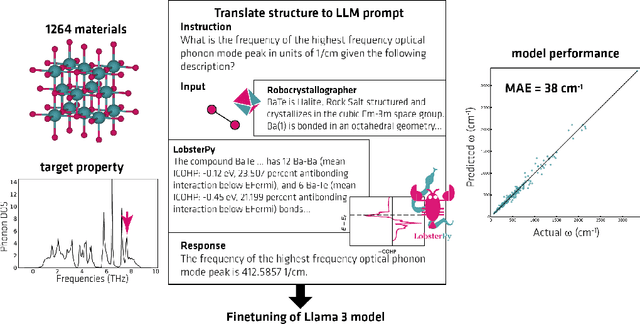
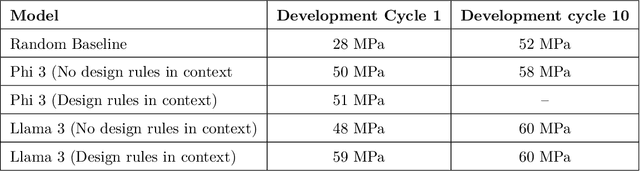
Here, we present the outcomes from the second Large Language Model (LLM) Hackathon for Applications in Materials Science and Chemistry, which engaged participants across global hybrid locations, resulting in 34 team submissions. The submissions spanned seven key application areas and demonstrated the diverse utility of LLMs for applications in (1) molecular and material property prediction; (2) molecular and material design; (3) automation and novel interfaces; (4) scientific communication and education; (5) research data management and automation; (6) hypothesis generation and evaluation; and (7) knowledge extraction and reasoning from scientific literature. Each team submission is presented in a summary table with links to the code and as brief papers in the appendix. Beyond team results, we discuss the hackathon event and its hybrid format, which included physical hubs in Toronto, Montreal, San Francisco, Berlin, Lausanne, and Tokyo, alongside a global online hub to enable local and virtual collaboration. Overall, the event highlighted significant improvements in LLM capabilities since the previous year's hackathon, suggesting continued expansion of LLMs for applications in materials science and chemistry research. These outcomes demonstrate the dual utility of LLMs as both multipurpose models for diverse machine learning tasks and platforms for rapid prototyping custom applications in scientific research.

Comparison of two artificial neural networks trained for the surrogate modeling of stress in materially heterogeneous elastoplastic solids

The purpose of this work is the systematic comparison of the application of two artificial neural networks (ANNs) to the surrogate modeling of the stress field in materially heterogeneous periodic polycrystalline microstructures. The first ANN is a UNet-based convolutional neural network (CNN) for periodic data, and the second is based on Fourier neural operators (FNO). Both of these were trained, validated, and tested with results from the numerical solution of the boundary-value problem (BVP) for quasi-static mechanical equilibrium in periodic grain microstructures with square domains. More specifically, these ANNs were trained to correlate the spatial distribution of material properties with the equilibrium stress field under uniaxial tensile loading. The resulting trained ANNs (tANNs) calculate the stress field for a given microstructure on the order of 1000 (UNet) to 2500 (FNO) times faster than the numerical solution of the corresponding BVP. For microstructures in the test dataset, the FNO-based tANN, or simply FNO, is more accurate than its UNet-based counterpart; the normalized mean absolute error of different stress components for the former is 0.25-0.40% as compared to 1.41-2.15% for the latter. Errors in FNO are restricted to grain boundary regions, whereas the error in U-Net also comes from within the grain. In comparison to U-Net, errors in FNO are more robust to large variations in spatial resolution as well as small variations in grain density. On other hand, errors in U-Net are robust to variations in boundary box aspect ratio, whereas errors in FNO increase as the domain becomes rectangular. Both tANNs are however unable to reproduce strong stress gradients, especially around regions of stress concentration.