Gaussian Process Neurons Learn Stochastic Activation Functions

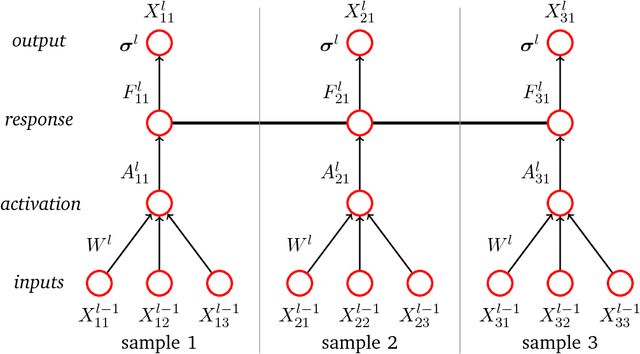
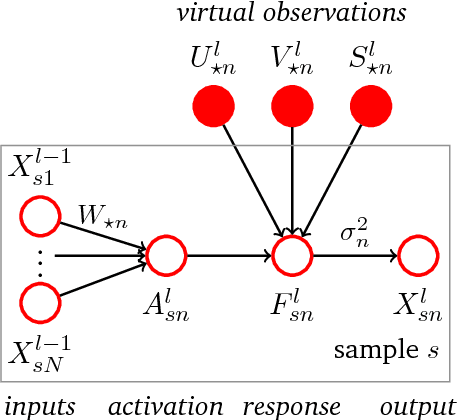
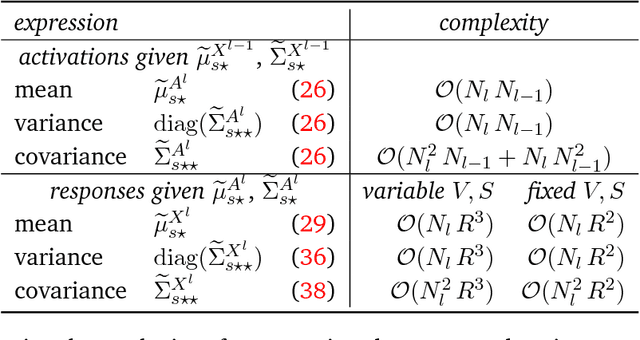
We propose stochastic, non-parametric activation functions that are fully learnable and individual to each neuron. Complexity and the risk of overfitting are controlled by placing a Gaussian process prior over these functions. The result is the Gaussian process neuron, a probabilistic unit that can be used as the basic building block for probabilistic graphical models that resemble the structure of neural networks. The proposed model can intrinsically handle uncertainties in its inputs and self-estimate the confidence of its predictions. Using variational Bayesian inference and the central limit theorem, a fully deterministic loss function is derived, allowing it to be trained as efficiently as a conventional neural network using mini-batch gradient descent. The posterior distribution of activation functions is inferred from the training data alongside the weights of the network. The proposed model favorably compares to deep Gaussian processes, both in model complexity and efficiency of inference. It can be directly applied to recurrent or convolutional network structures, allowing its use in audio and image processing tasks. As an preliminary empirical evaluation we present experiments on regression and classification tasks, in which our model achieves performance comparable to or better than a Dropout regularized neural network with a fixed activation function. Experiments are ongoing and results will be added as they become available.

Automatic Differentiation for Tensor Algebras

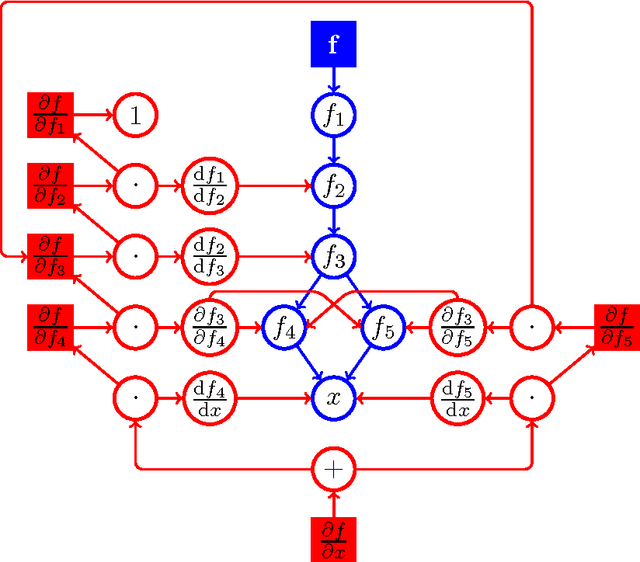
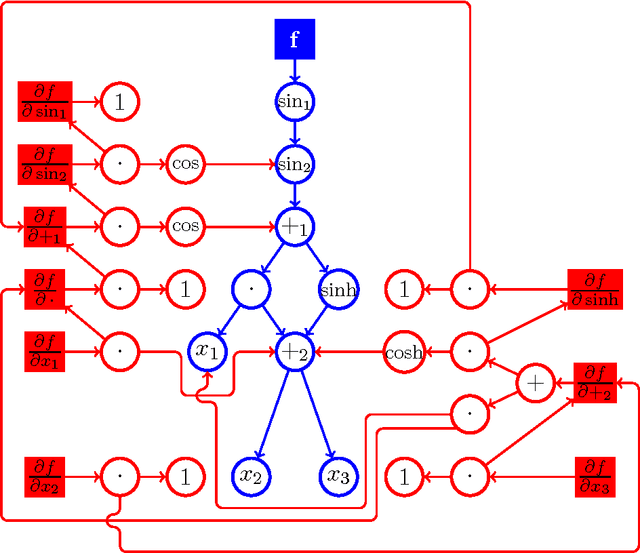
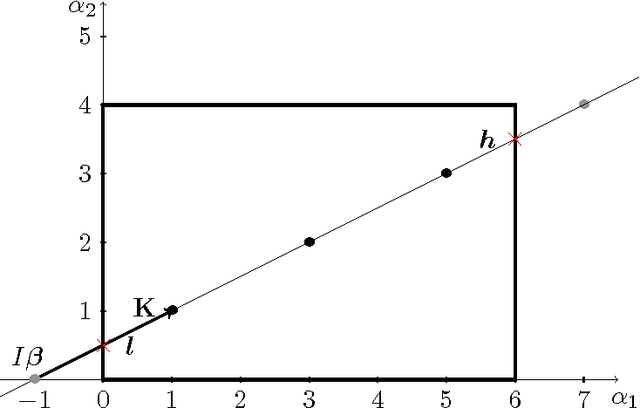
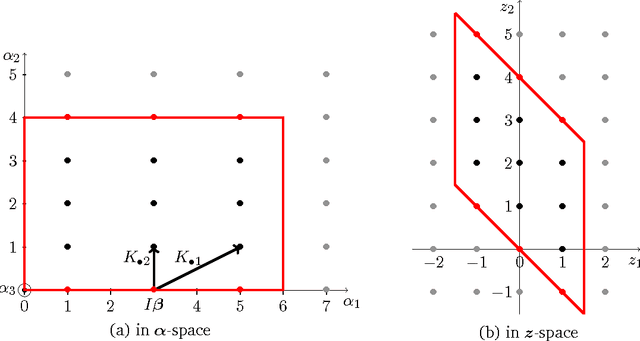
Kjolstad et. al. proposed a tensor algebra compiler. It takes expressions that define a tensor element-wise, such as $f_{ij}(a,b,c,d) = \exp\left[-\sum_{k=0}^4 \left((a_{ik}+b_{jk})^2\, c_{ii} + d_{i+k}^3 \right) \right]$, and generates the corresponding compute kernel code. For machine learning, especially deep learning, it is often necessary to compute the gradient of a loss function $l(a,b,c,d)=l(f(a,b,c,d))$ with respect to parameters $a,b,c,d$. If tensor compilers are to be applied in this field, it is necessary to derive expressions for the derivatives of element-wise defined tensors, i.e. expressions for $(da)_{ik}=\partial l/\partial a_{ik}$. When the mapping between function indices and argument indices is not 1:1, special attention is required. For the function $f_{ij} (x) = x_i^2$, the derivative of the loss is $(dx)_i=\partial l/\partial x_i=\sum_j (df)_{ij}2x_i$; the sum is necessary because index $j$ does not appear in the indices of $f$. Another example is $f_{i}(x)=x_{ii}^2$, where $x$ is a matrix; here we have $(dx)_{ij}=\delta_{ij}(df)_i2x_{ii}$; the Kronecker delta is necessary because the derivative is zero for off-diagonal elements. Another indexing scheme is used by $f_{ij}(x)=\exp x_{i+j}$; here the correct derivative is $(dx)_{k}=\sum_i (df)_{i,k-i} \exp x_{k}$, where the range of the sum must be chosen appropriately. In this publication we present an algorithm that can handle any case in which the indices of an argument are an arbitrary linear combination of the indices of the function, thus all the above examples can be handled. Sums (and their ranges) and Kronecker deltas are automatically inserted into the derivatives as necessary. Additionally, the indices are transformed, if required (as in the last example). The algorithm outputs a symbolic expression that can be subsequently fed into a tensor algebra compiler. Source code is provided.

Theano: A Python framework for fast computation of mathematical expressions

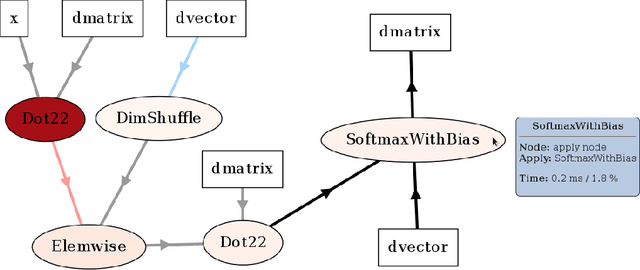
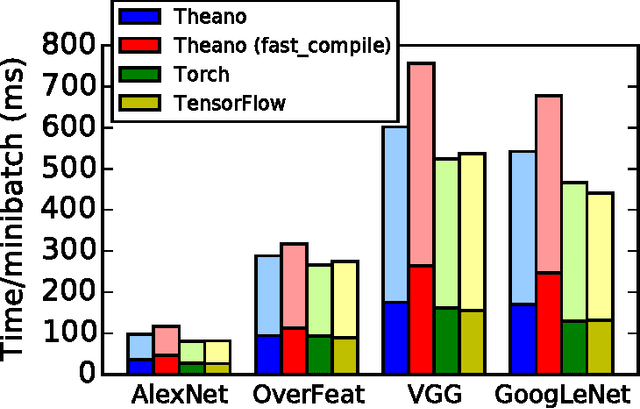
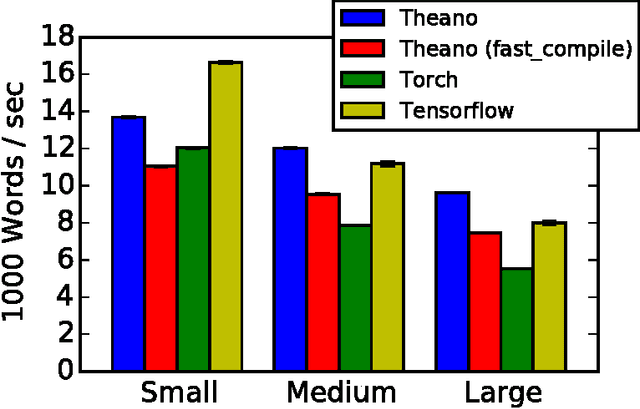
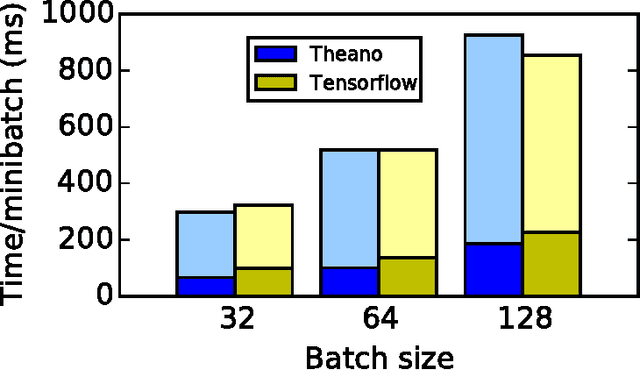
Theano is a Python library that allows to define, optimize, and evaluate mathematical expressions involving multi-dimensional arrays efficiently. Since its introduction, it has been one of the most used CPU and GPU mathematical compilers - especially in the machine learning community - and has shown steady performance improvements. Theano is being actively and continuously developed since 2008, multiple frameworks have been built on top of it and it has been used to produce many state-of-the-art machine learning models. The present article is structured as follows. Section I provides an overview of the Theano software and its community. Section II presents the principal features of Theano and how to use them, and compares them with other similar projects. Section III focuses on recently-introduced functionalities and improvements. Section IV compares the performance of Theano against Torch7 and TensorFlow on several machine learning models. Section V discusses current limitations of Theano and potential ways of improving it.

A Differentiable Transition Between Additive and Multiplicative Neurons

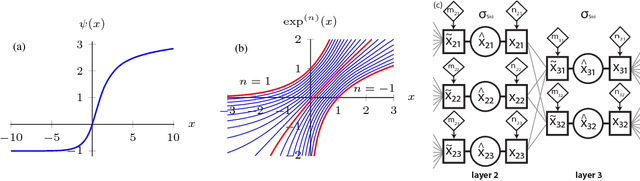
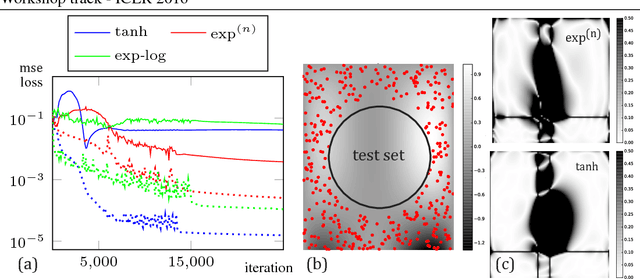
Existing approaches to combine both additive and multiplicative neural units either use a fixed assignment of operations or require discrete optimization to determine what function a neuron should perform. However, this leads to an extensive increase in the computational complexity of the training procedure. We present a novel, parameterizable transfer function based on the mathematical concept of non-integer functional iteration that allows the operation each neuron performs to be smoothly and, most importantly, differentiablely adjusted between addition and multiplication. This allows the decision between addition and multiplication to be integrated into the standard backpropagation training procedure.

A Neural Transfer Function for a Smooth and Differentiable Transition Between Additive and Multiplicative Interactions

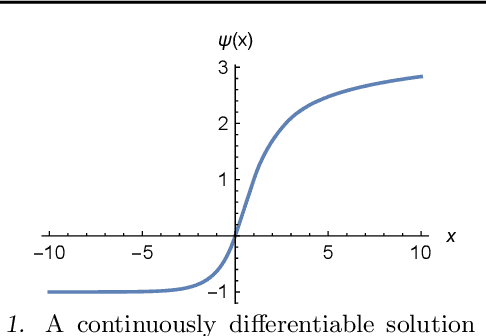
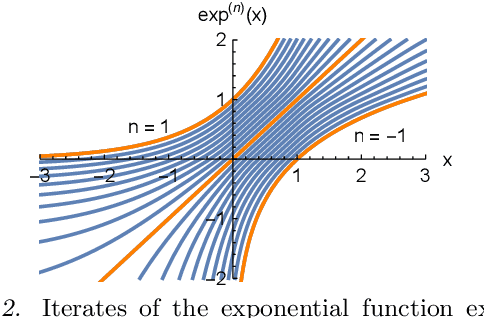
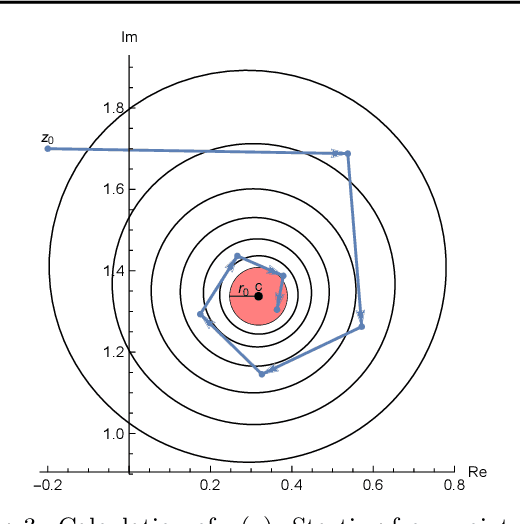
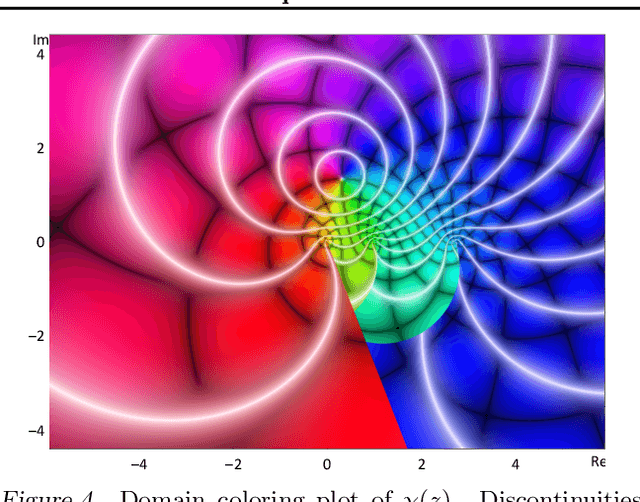
Existing approaches to combine both additive and multiplicative neural units either use a fixed assignment of operations or require discrete optimization to determine what function a neuron should perform. This leads either to an inefficient distribution of computational resources or an extensive increase in the computational complexity of the training procedure. We present a novel, parameterizable transfer function based on the mathematical concept of non-integer functional iteration that allows the operation each neuron performs to be smoothly and, most importantly, differentiablely adjusted between addition and multiplication. This allows the decision between addition and multiplication to be integrated into the standard backpropagation training procedure.

On Fast Dropout and its Applicability to Recurrent Networks

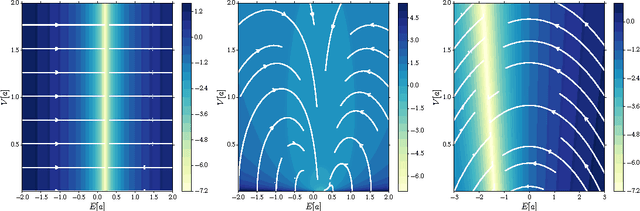
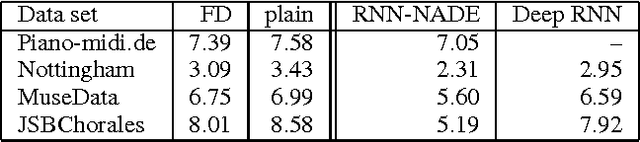
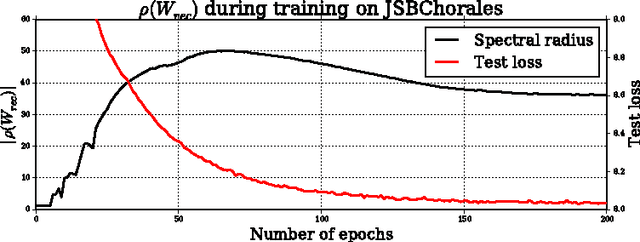
Recurrent Neural Networks (RNNs) are rich models for the processing of sequential data. Recent work on advancing the state of the art has been focused on the optimization or modelling of RNNs, mostly motivated by adressing the problems of the vanishing and exploding gradients. The control of overfitting has seen considerably less attention. This paper contributes to that by analyzing fast dropout, a recent regularization method for generalized linear models and neural networks from a back-propagation inspired perspective. We show that fast dropout implements a quadratic form of an adaptive, per-parameter regularizer, which rewards large weights in the light of underfitting, penalizes them for overconfident predictions and vanishes at minima of an unregularized training loss. The derivatives of that regularizer are exclusively based on the training error signal. One consequence of this is the absense of a global weight attractor, which is particularly appealing for RNNs, since the dynamics are not biased towards a certain regime. We positively test the hypothesis that this improves the performance of RNNs on four musical data sets.

Unsupervised Feature Learning for low-level Local Image Descriptors

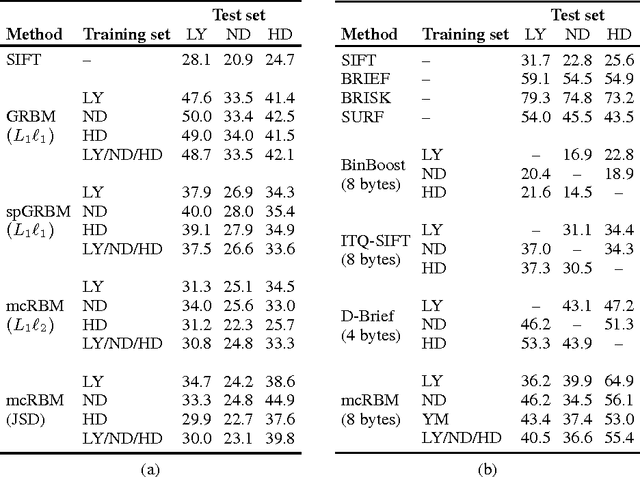
Unsupervised feature learning has shown impressive results for a wide range of input modalities, in particular for object classification tasks in computer vision. Using a large amount of unlabeled data, unsupervised feature learning methods are utilized to construct high-level representations that are discriminative enough for subsequently trained supervised classification algorithms. However, it has never been \emph{quantitatively} investigated yet how well unsupervised learning methods can find \emph{low-level representations} for image patches without any additional supervision. In this paper we examine the performance of pure unsupervised methods on a low-level correspondence task, a problem that is central to many Computer Vision applications. We find that a special type of Restricted Boltzmann Machines (RBMs) performs comparably to hand-crafted descriptors. Additionally, a simple binarization scheme produces compact representations that perform better than several state-of-the-art descriptors.