Fast Adaptive Weight Noise

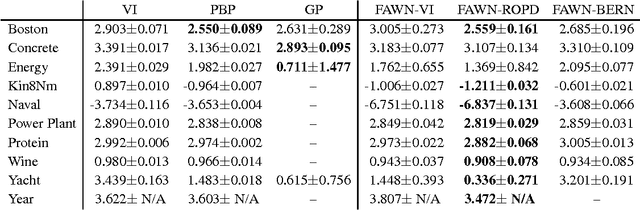
Marginalising out uncertain quantities within the internal representations or parameters of neural networks is of central importance for a wide range of learning techniques, such as empirical, variational or full Bayesian methods. We set out to generalise fast dropout (Wang & Manning, 2013) to cover a wider variety of noise processes in neural networks. This leads to an efficient calculation of the marginal likelihood and predictive distribution which evades sampling and the consequential increase in training time due to highly variant gradient estimates. This allows us to approximate variational Bayes for the parameters of feed-forward neural networks. Inspired by the minimum description length principle, we also propose and experimentally verify the direct optimisation of the regularised predictive distribution. The methods yield results competitive with previous neural network based approaches and Gaussian processes on a wide range of regression tasks.

On Fast Dropout and its Applicability to Recurrent Networks

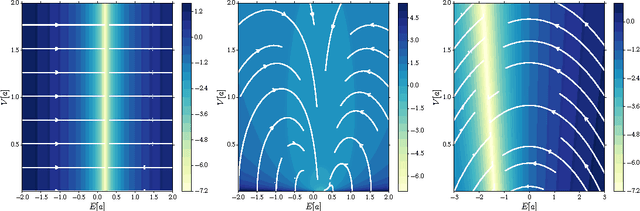
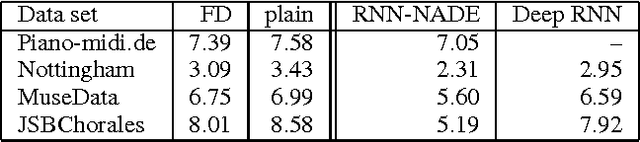
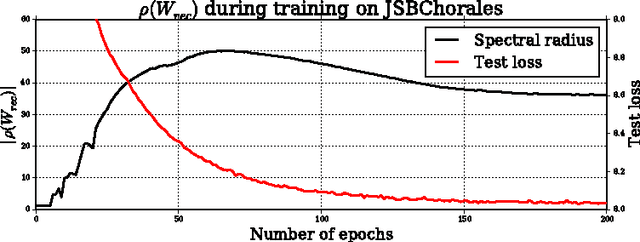
Recurrent Neural Networks (RNNs) are rich models for the processing of sequential data. Recent work on advancing the state of the art has been focused on the optimization or modelling of RNNs, mostly motivated by adressing the problems of the vanishing and exploding gradients. The control of overfitting has seen considerably less attention. This paper contributes to that by analyzing fast dropout, a recent regularization method for generalized linear models and neural networks from a back-propagation inspired perspective. We show that fast dropout implements a quadratic form of an adaptive, per-parameter regularizer, which rewards large weights in the light of underfitting, penalizes them for overconfident predictions and vanishes at minima of an unregularized training loss. The derivatives of that regularizer are exclusively based on the training error signal. One consequence of this is the absense of a global weight attractor, which is particularly appealing for RNNs, since the dynamics are not biased towards a certain regime. We positively test the hypothesis that this improves the performance of RNNs on four musical data sets.