Fast Adaptive Weight Noise
Paper and Code
Jul 19, 2015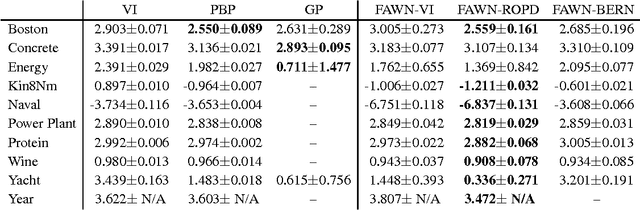
Marginalising out uncertain quantities within the internal representations or parameters of neural networks is of central importance for a wide range of learning techniques, such as empirical, variational or full Bayesian methods. We set out to generalise fast dropout (Wang & Manning, 2013) to cover a wider variety of noise processes in neural networks. This leads to an efficient calculation of the marginal likelihood and predictive distribution which evades sampling and the consequential increase in training time due to highly variant gradient estimates. This allows us to approximate variational Bayes for the parameters of feed-forward neural networks. Inspired by the minimum description length principle, we also propose and experimentally verify the direct optimisation of the regularised predictive distribution. The methods yield results competitive with previous neural network based approaches and Gaussian processes on a wide range of regression tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge