Towards Compositional Interpretability for XAI

Artificial intelligence (AI) is currently based largely on black-box machine learning models which lack interpretability. The field of eXplainable AI (XAI) strives to address this major concern, being critical in high-stakes areas such as the finance, legal and health sectors. We present an approach to defining AI models and their interpretability based on category theory. For this we employ the notion of a compositional model, which sees a model in terms of formal string diagrams which capture its abstract structure together with its concrete implementation. This comprehensive view incorporates deterministic, probabilistic and quantum models. We compare a wide range of AI models as compositional models, including linear and rule-based models, (recurrent) neural networks, transformers, VAEs, and causal and DisCoCirc models. Next we give a definition of interpretation of a model in terms of its compositional structure, demonstrating how to analyse the interpretability of a model, and using this to clarify common themes in XAI. We find that what makes the standard 'intrinsically interpretable' models so transparent is brought out most clearly diagrammatically. This leads us to the more general notion of compositionally-interpretable (CI) models, which additionally include, for instance, causal, conceptual space, and DisCoCirc models. We next demonstrate the explainability benefits of CI models. Firstly, their compositional structure may allow the computation of other quantities of interest, and may facilitate inference from the model to the modelled phenomenon by matching its structure. Secondly, they allow for diagrammatic explanations for their behaviour, based on influence constraints, diagram surgery and rewrite explanations. Finally, we discuss many future directions for the approach, raising the question of how to learn such meaningfully structured models in practice.

Active Inference in String Diagrams: A Categorical Account of Predictive Processing and Free Energy

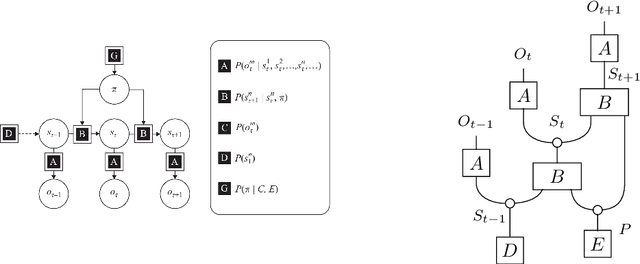
We present a categorical formulation of the cognitive frameworks of Predictive Processing and Active Inference, expressed in terms of string diagrams interpreted in a monoidal category with copying and discarding. This includes diagrammatic accounts of generative models, Bayesian updating, perception, planning, active inference, and free energy. In particular we present a diagrammatic derivation of the formula for active inference via free energy minimisation, and establish a compositionality property for free energy, allowing free energy to be applied at all levels of an agent's generative model. Aside from aiming to provide a helpful graphical language for those familiar with active inference, we conversely hope that this article may provide a concise formulation and introduction to the framework.

Causal models in string diagrams

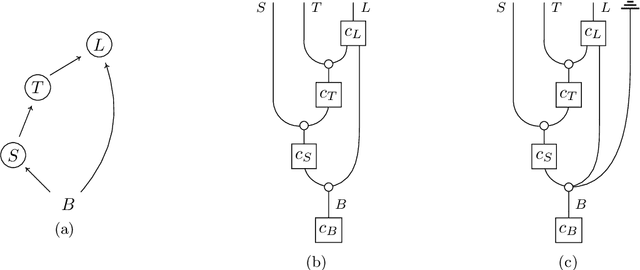
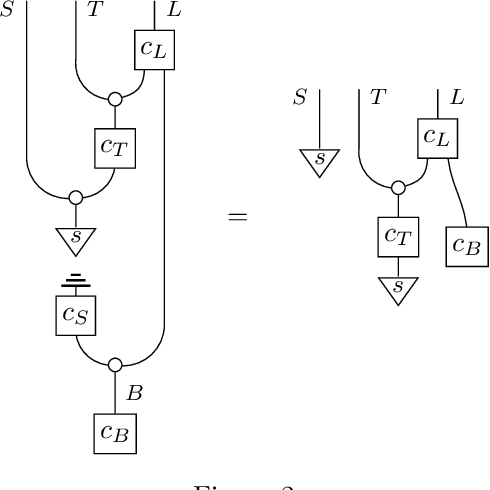
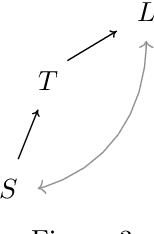
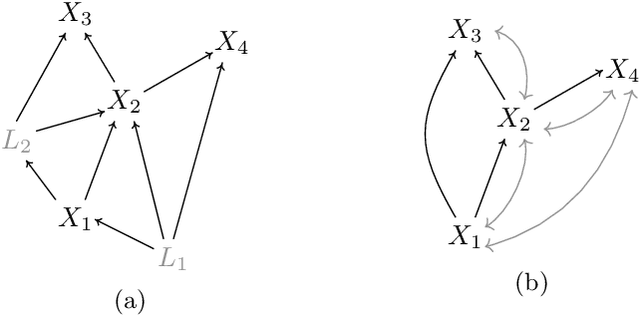
The framework of causal models provides a principled approach to causal reasoning, applied today across many scientific domains. Here we present this framework in the language of string diagrams, interpreted formally using category theory. A class of string diagrams, called network diagrams, are in 1-to-1 correspondence with directed acyclic graphs. A causal model is given by such a diagram with its components interpreted as stochastic maps, functions, or general channels in a symmetric monoidal category with a 'copy-discard' structure (cd-category), turning a model into a single mathematical object that can be reasoned with intuitively and yet rigorously. Building on prior works by Fong and Jacobs, Kissinger and Zanasi, as well as Fritz and Klingler, we present diagrammatic definitions of causal models and functional causal models in a cd-category, generalising causal Bayesian networks and structural causal models, respectively. We formalise general interventions on a model, including but beyond do-interventions, and present the natural notion of an open causal model with inputs. We also give an approach to conditioning based on a normalisation box, allowing for causal inference calculations to be done fully diagrammatically. We define counterfactuals in this setup, and treat the problems of the identifiability of causal effects and counterfactuals fully diagrammatically. The benefits of such a presentation of causal models lie in foundational questions in causal reasoning and in their clarificatory role and pedagogical value. This work aims to be accessible to different communities, from causal model practitioners to researchers in applied category theory, and discusses many examples from the literature for illustration. Overall, we argue and demonstrate that causal reasoning according to the causal model framework is most naturally and intuitively done as diagrammatic reasoning.

Formalising and Learning a Quantum Model of Concepts

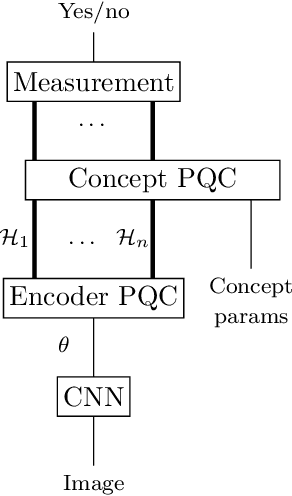
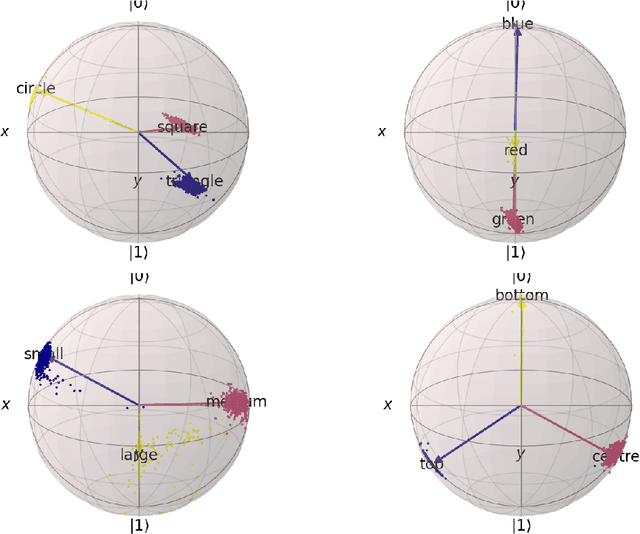
In this report we present a new modelling framework for concepts based on quantum theory, and demonstrate how the conceptual representations can be learned automatically from data. A contribution of the work is a thorough category-theoretic formalisation of our framework. We claim that the use of category theory, and in particular the use of string diagrams to describe quantum processes, helps elucidate some of the most important features of our quantum approach to concept modelling. Our approach builds upon Gardenfors' classical framework of conceptual spaces, in which cognition is modelled geometrically through the use of convex spaces, which in turn factorise in terms of simpler spaces called domains. We show how concepts from the domains of shape, colour, size and position can be learned from images of simple shapes, where individual images are represented as quantum states and concepts as quantum effects. Concepts are learned by a hybrid classical-quantum network trained to perform concept classification, where the classical image processing is carried out by a convolutional neural network and the quantum representations are produced by a parameterised quantum circuit. We also use discarding to produce mixed effects, which can then be used to learn concepts which only apply to a subset of the domains, and show how entanglement (together with discarding) can be used to capture interesting correlations across domains. Finally, we consider the question of whether our quantum models of concepts can be considered conceptual spaces in the Gardenfors sense.

The Conceptual VAE

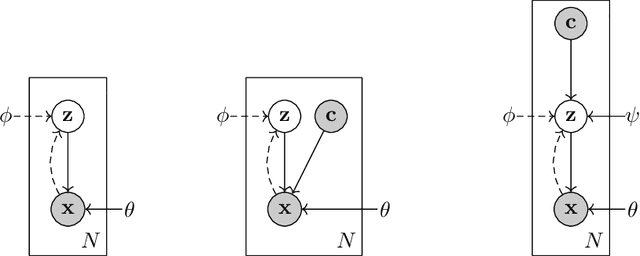
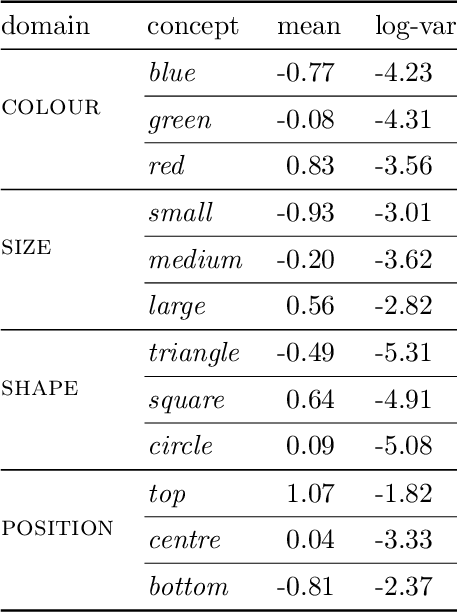
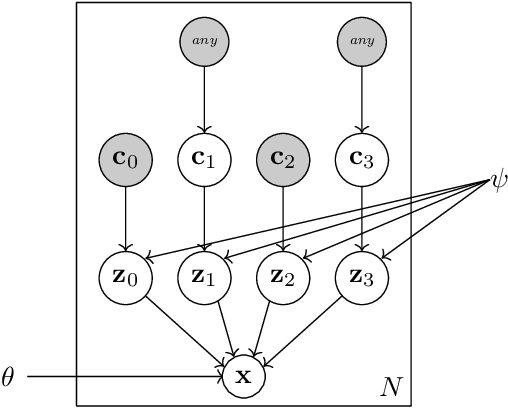
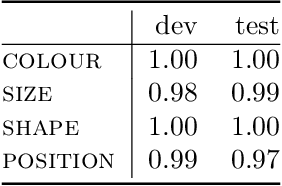
In this report we present a new model of concepts, based on the framework of variational autoencoders, which is designed to have attractive properties such as factored conceptual domains, and at the same time be learnable from data. The model is inspired by, and closely related to, the Beta-VAE model of concepts, but is designed to be more closely connected with language, so that the names of concepts form part of the graphical model. We provide evidence that our model -- which we call the Conceptual VAE -- is able to learn interpretable conceptual representations from simple images of coloured shapes together with the corresponding concept labels. We also show how the model can be used as a concept classifier, and how it can be adapted to learn from fewer labels per instance. Finally, we formally relate our model to Gardenfors' theory of conceptual spaces, showing how the Gaussians we use to represent concepts can be formalised in terms of "fuzzy concepts" in such a space.

A Categorical Semantics of Fuzzy Concepts in Conceptual Spaces

We define a symmetric monoidal category modelling fuzzy concepts and fuzzy conceptual reasoning within G\"ardenfors' framework of conceptual (convex) spaces. We propose log-concave functions as models of fuzzy concepts, showing that these are the most general choice satisfying a criterion due to G\"ardenfors and which are well-behaved compositionally. We then generalise these to define the category of log-concave probabilistic channels between convex spaces, which allows one to model fuzzy reasoning with noisy inputs, and provides a novel example of a Markov category.

The Mathematical Structure of Integrated Information Theory

Integrated Information Theory is one of the leading models of consciousness. It aims to describe both the quality and quantity of the conscious experience of a physical system, such as the brain, in a particular state. In this contribution, we propound the mathematical structure of the theory, separating the essentials from auxiliary formal tools. We provide a definition of a generalized IIT which has IIT 3.0 of Tononi et. al., as well as the Quantum IIT introduced by Zanardi et. al. as special cases. This provides an axiomatic definition of the theory which may serve as the starting point for future formal investigations and as an introduction suitable for researchers with a formal background.