Causal models in string diagrams
Paper and Code
Apr 15, 2023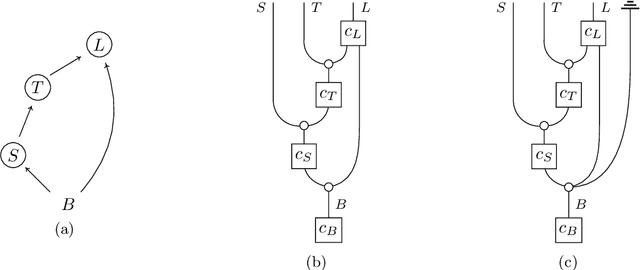
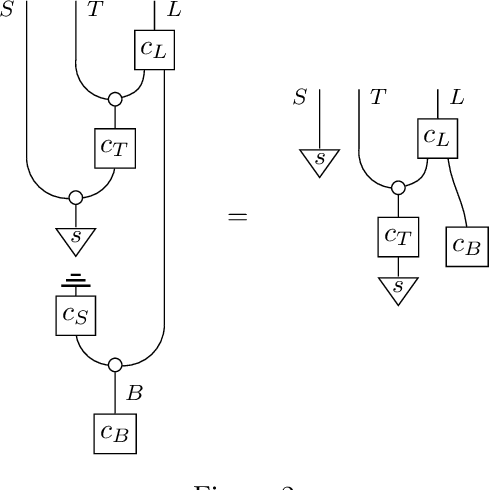
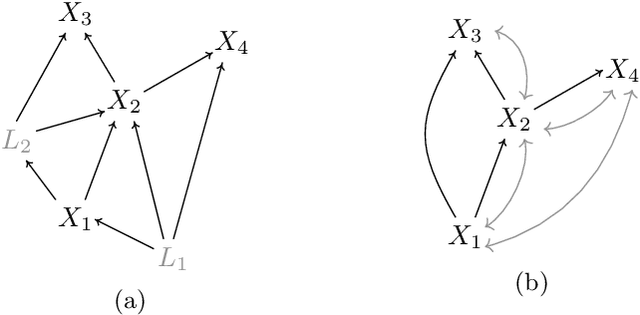
The framework of causal models provides a principled approach to causal reasoning, applied today across many scientific domains. Here we present this framework in the language of string diagrams, interpreted formally using category theory. A class of string diagrams, called network diagrams, are in 1-to-1 correspondence with directed acyclic graphs. A causal model is given by such a diagram with its components interpreted as stochastic maps, functions, or general channels in a symmetric monoidal category with a 'copy-discard' structure (cd-category), turning a model into a single mathematical object that can be reasoned with intuitively and yet rigorously. Building on prior works by Fong and Jacobs, Kissinger and Zanasi, as well as Fritz and Klingler, we present diagrammatic definitions of causal models and functional causal models in a cd-category, generalising causal Bayesian networks and structural causal models, respectively. We formalise general interventions on a model, including but beyond do-interventions, and present the natural notion of an open causal model with inputs. We also give an approach to conditioning based on a normalisation box, allowing for causal inference calculations to be done fully diagrammatically. We define counterfactuals in this setup, and treat the problems of the identifiability of causal effects and counterfactuals fully diagrammatically. The benefits of such a presentation of causal models lie in foundational questions in causal reasoning and in their clarificatory role and pedagogical value. This work aims to be accessible to different communities, from causal model practitioners to researchers in applied category theory, and discusses many examples from the literature for illustration. Overall, we argue and demonstrate that causal reasoning according to the causal model framework is most naturally and intuitively done as diagrammatic reasoning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge