Toward Pareto Efficient Fairness-Utility Trade-off inRecommendation through Reinforcement Learning

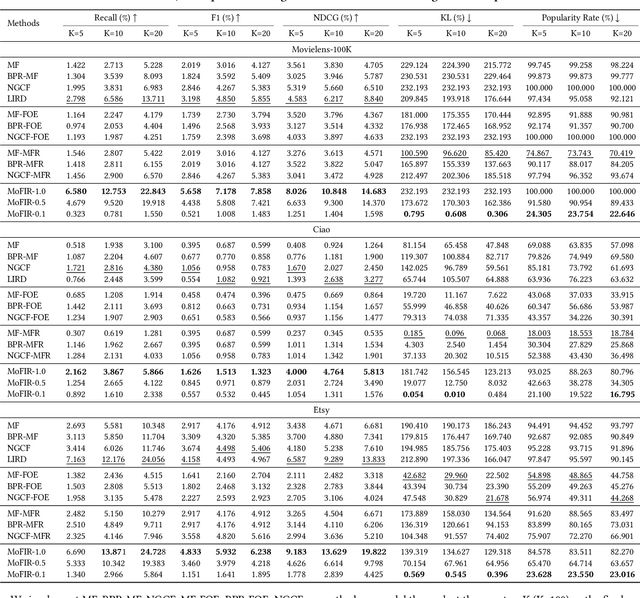
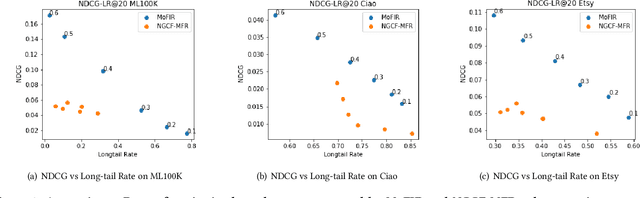
The issue of fairness in recommendation is becoming increasingly essential as Recommender Systems touch and influence more and more people in their daily lives. In fairness-aware recommendation, most of the existing algorithmic approaches mainly aim at solving a constrained optimization problem by imposing a constraint on the level of fairness while optimizing the main recommendation objective, e.g., CTR. While this alleviates the impact of unfair recommendations, the expected return of an approach may significantly compromise the recommendation accuracy due to the inherent trade-off between fairness and utility. This motivates us to deal with these conflicting objectives and explore the optimal trade-off between them in recommendation. One conspicuous approach is to seek a Pareto efficient solution to guarantee optimal compromises between utility and fairness. Moreover, considering the needs of real-world e-commerce platforms, it would be more desirable if we can generalize the whole Pareto Frontier, so that the decision-makers can specify any preference of one objective over another based on their current business needs. Therefore, in this work, we propose a fairness-aware recommendation framework using multi-objective reinforcement learning, called MoFIR, which is able to learn a single parametric representation for optimal recommendation policies over the space of all possible preferences. Specially, we modify traditional DDPG by introducing conditioned network into it, which conditions the networks directly on these preferences and outputs Q-value-vectors. Experiments on several real-world recommendation datasets verify the superiority of our framework on both fairness metrics and recommendation measures when compared with all other baselines. We also extract the approximate Pareto Frontier on real-world datasets generated by MoFIR and compare to state-of-the-art fairness methods.

Feature Selection for Ridge Regression with Provable Guarantees

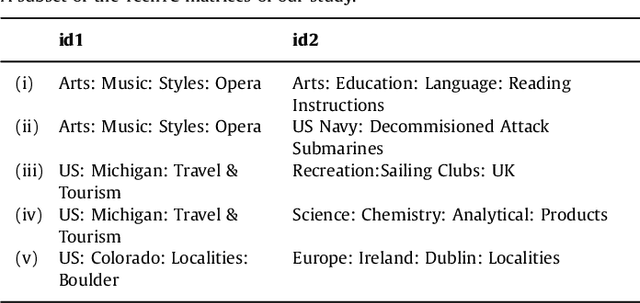
We introduce single-set spectral sparsification as a deterministic sampling based feature selection technique for regularized least squares classification, which is the classification analogue to ridge regression. The method is unsupervised and gives worst-case guarantees of the generalization power of the classification function after feature selection with respect to the classification function obtained using all features. We also introduce leverage-score sampling as an unsupervised randomized feature selection method for ridge regression. We provide risk bounds for both single-set spectral sparsification and leverage-score sampling on ridge regression in the fixed design setting and show that the risk in the sampled space is comparable to the risk in the full-feature space. We perform experiments on synthetic and real-world datasets, namely a subset of TechTC-300 datasets, to support our theory. Experimental results indicate that the proposed methods perform better than the existing feature selection methods.

Feature Selection for Linear SVM with Provable Guarantees

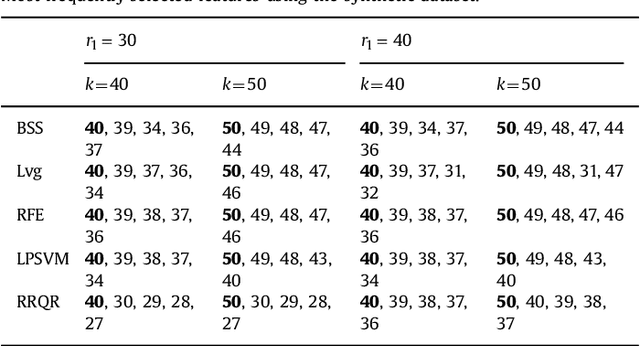
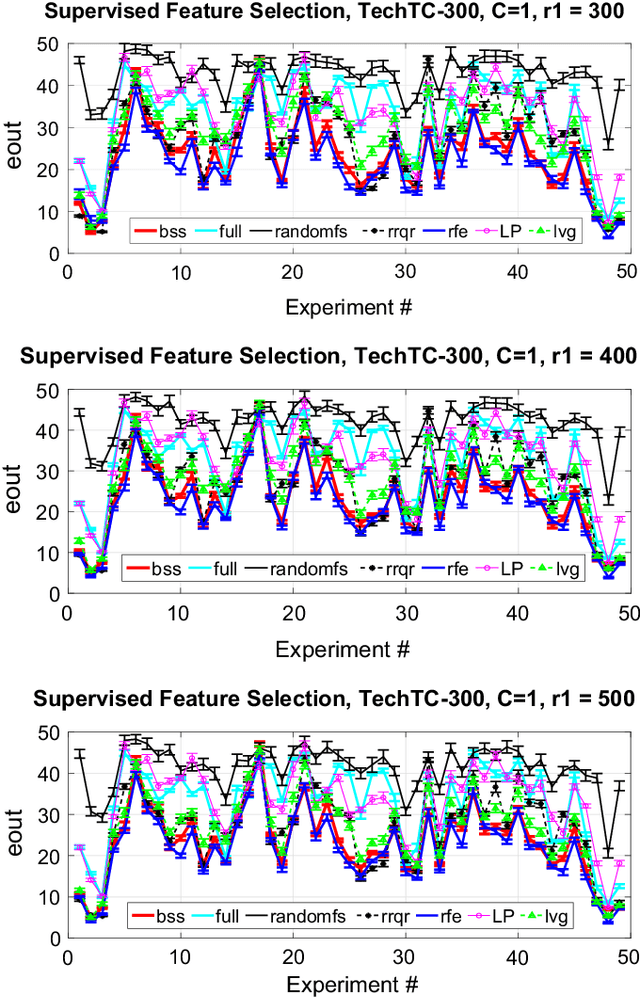
We give two provably accurate feature-selection techniques for the linear SVM. The algorithms run in deterministic and randomized time respectively. Our algorithms can be used in an unsupervised or supervised setting. The supervised approach is based on sampling features from support vectors. We prove that the margin in the feature space is preserved to within $\epsilon$-relative error of the margin in the full feature space in the worst-case. In the unsupervised setting, we also provide worst-case guarantees of the radius of the minimum enclosing ball, thereby ensuring comparable generalization as in the full feature space and resolving an open problem posed in Dasgupta et al. We present extensive experiments on real-world datasets to support our theory and to demonstrate that our method is competitive and often better than prior state-of-the-art, for which there are no known provable guarantees.

Random Projections for Linear Support Vector Machines

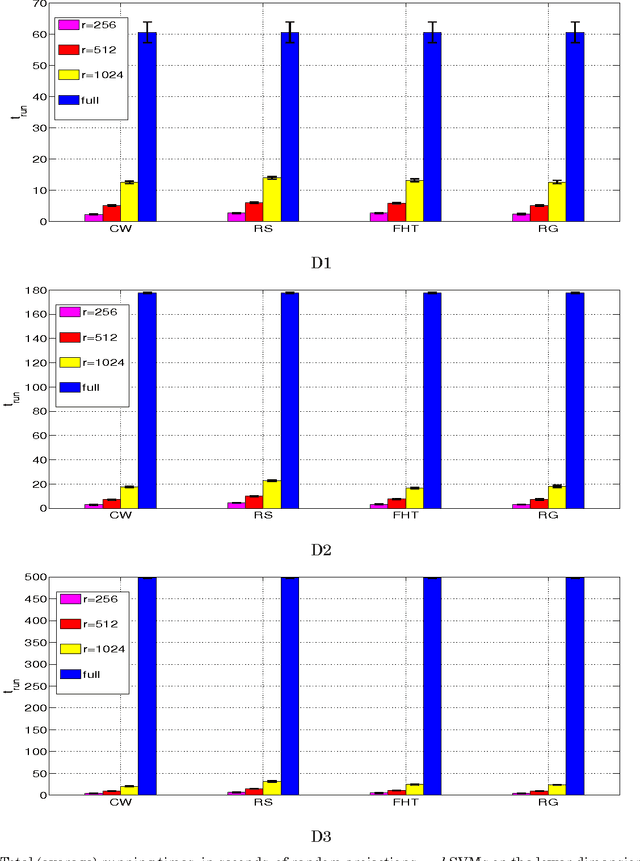
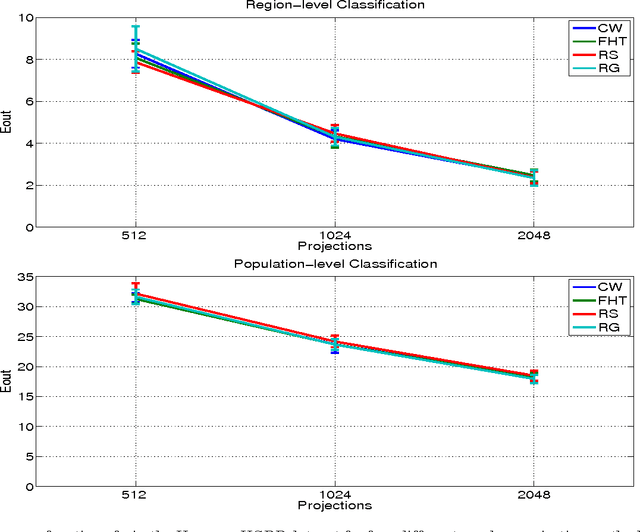
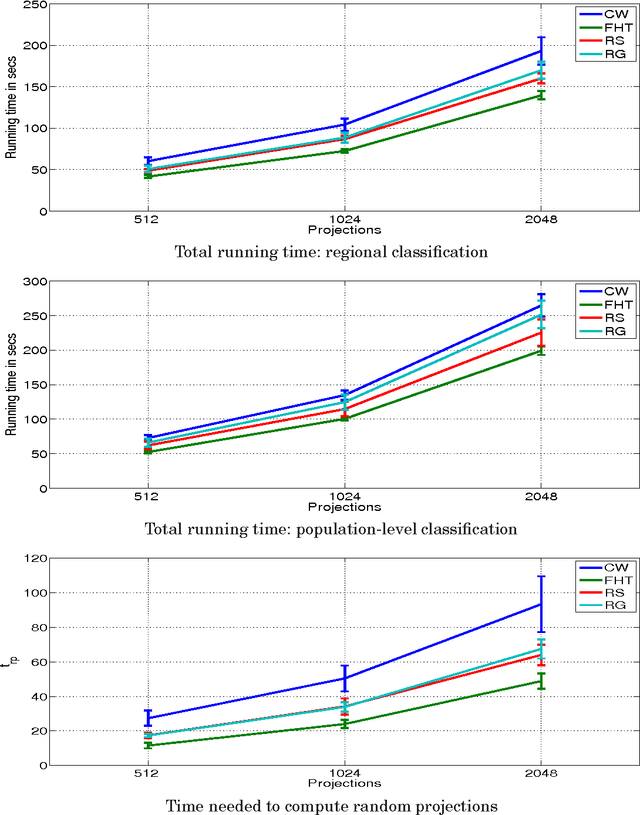
Let X be a data matrix of rank \rho, whose rows represent n points in d-dimensional space. The linear support vector machine constructs a hyperplane separator that maximizes the 1-norm soft margin. We develop a new oblivious dimension reduction technique which is precomputed and can be applied to any input matrix X. We prove that, with high probability, the margin and minimum enclosing ball in the feature space are preserved to within \epsilon-relative error, ensuring comparable generalization as in the original space in the case of classification. For regression, we show that the margin is preserved to \epsilon-relative error with high probability. We present extensive experiments with real and synthetic data to support our theory.