Spectral Clustering via the Power Method -- Provably

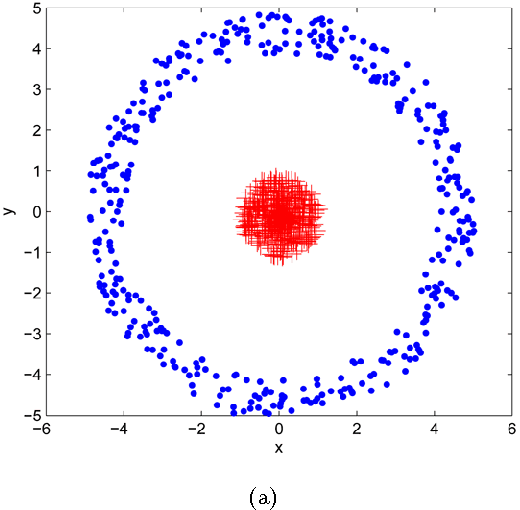
Spectral clustering is one of the most important algorithms in data mining and machine intelligence; however, its computational complexity limits its application to truly large scale data analysis. The computational bottleneck in spectral clustering is computing a few of the top eigenvectors of the (normalized) Laplacian matrix corresponding to the graph representing the data to be clustered. One way to speed up the computation of these eigenvectors is to use the "power method" from the numerical linear algebra literature. Although the power method has been empirically used to speed up spectral clustering, the theory behind this approach, to the best of our knowledge, remains unexplored. This paper provides the \emph{first} such rigorous theoretical justification, arguing that a small number of power iterations suffices to obtain near-optimal partitionings using the approximate eigenvectors. Specifically, we prove that solving the $k$-means clustering problem on the approximate eigenvectors obtained via the power method gives an additive-error approximation to solving the $k$-means problem on the optimal eigenvectors.

Optimal Sparse Linear Auto-Encoders and Sparse PCA

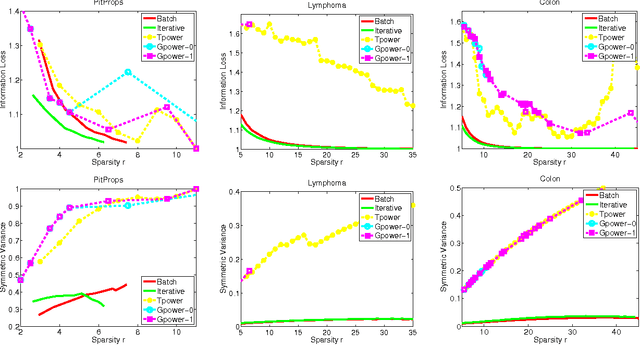
Principal components analysis (PCA) is the optimal linear auto-encoder of data, and it is often used to construct features. Enforcing sparsity on the principal components can promote better generalization, while improving the interpretability of the features. We study the problem of constructing optimal sparse linear auto-encoders. Two natural questions in such a setting are: i) Given a level of sparsity, what is the best approximation to PCA that can be achieved? ii) Are there low-order polynomial-time algorithms which can asymptotically achieve this optimal tradeoff between the sparsity and the approximation quality? In this work, we answer both questions by giving efficient low-order polynomial-time algorithms for constructing asymptotically \emph{optimal} linear auto-encoders (in particular, sparse features with near-PCA reconstruction error) and demonstrate the performance of our algorithms on real data.

Randomized Dimensionality Reduction for k-means Clustering

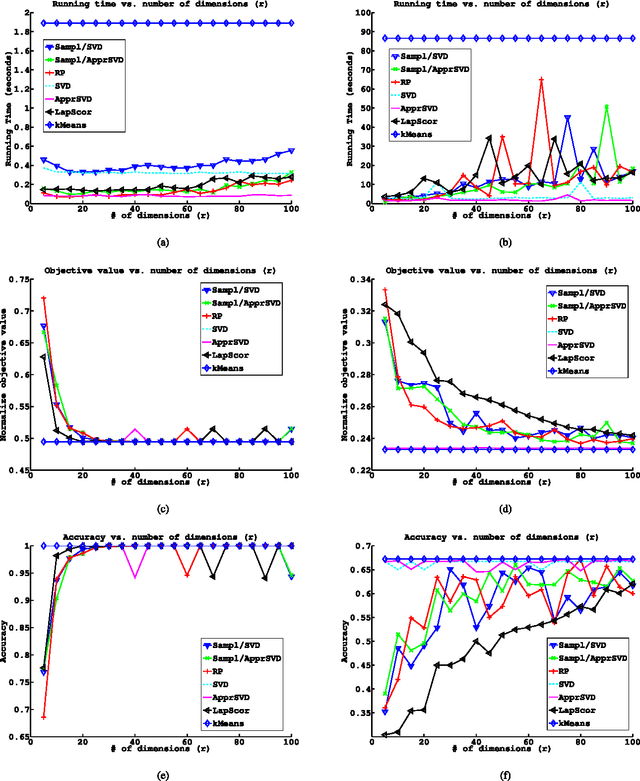
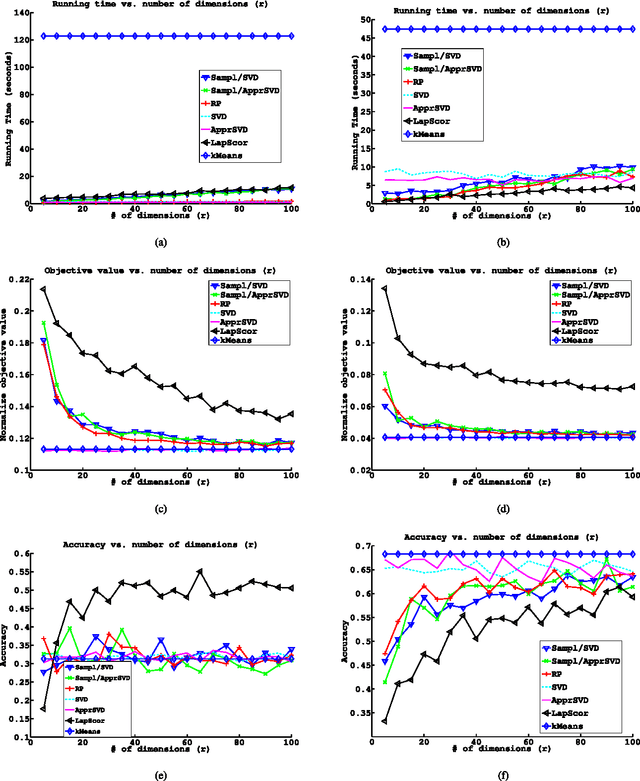
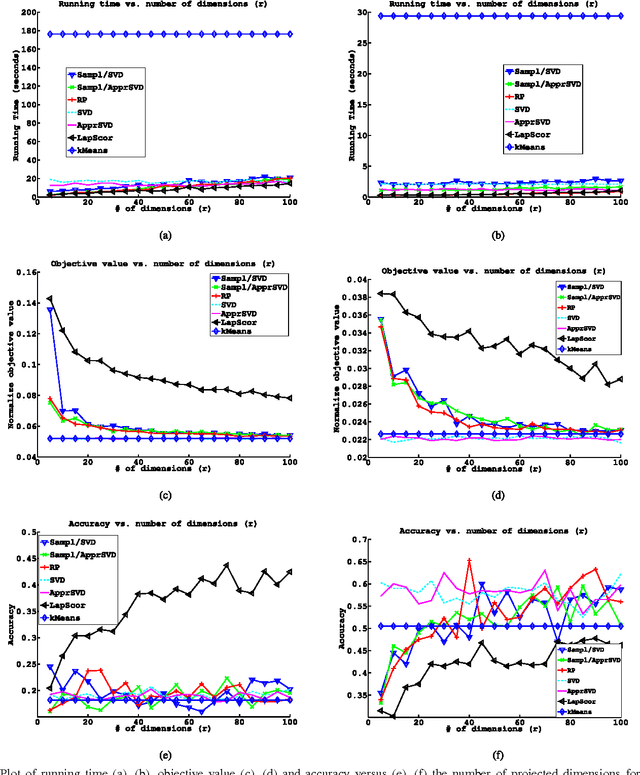
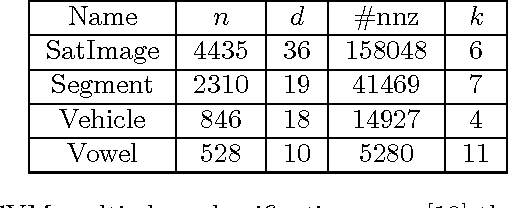
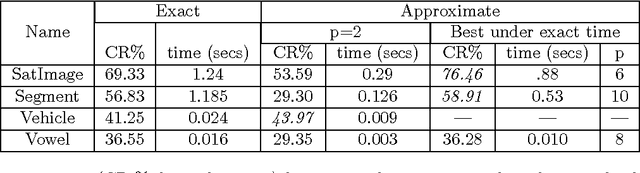
We study the topic of dimensionality reduction for $k$-means clustering. Dimensionality reduction encompasses the union of two approaches: \emph{feature selection} and \emph{feature extraction}. A feature selection based algorithm for $k$-means clustering selects a small subset of the input features and then applies $k$-means clustering on the selected features. A feature extraction based algorithm for $k$-means clustering constructs a small set of new artificial features and then applies $k$-means clustering on the constructed features. Despite the significance of $k$-means clustering as well as the wealth of heuristic methods addressing it, provably accurate feature selection methods for $k$-means clustering are not known. On the other hand, two provably accurate feature extraction methods for $k$-means clustering are known in the literature; one is based on random projections and the other is based on the singular value decomposition (SVD). This paper makes further progress towards a better understanding of dimensionality reduction for $k$-means clustering. Namely, we present the first provably accurate feature selection method for $k$-means clustering and, in addition, we present two feature extraction methods. The first feature extraction method is based on random projections and it improves upon the existing results in terms of time complexity and number of features needed to be extracted. The second feature extraction method is based on fast approximate SVD factorizations and it also improves upon the existing results in terms of time complexity. The proposed algorithms are randomized and provide constant-factor approximation guarantees with respect to the optimal $k$-means objective value.

Optimal CUR Matrix Decompositions

The CUR decomposition of an $m \times n$ matrix $A$ finds an $m \times c$ matrix $C$ with a subset of $c < n$ columns of $A,$ together with an $r \times n$ matrix $R$ with a subset of $r < m$ rows of $A,$ as well as a $c \times r$ low-rank matrix $U$ such that the matrix $C U R$ approximates the matrix $A,$ that is, $ || A - CUR ||_F^2 \le (1+\epsilon) || A - A_k||_F^2$, where $||.||_F$ denotes the Frobenius norm and $A_k$ is the best $m \times n$ matrix of rank $k$ constructed via the SVD. We present input-sparsity-time and deterministic algorithms for constructing such a CUR decomposition where $c=O(k/\epsilon)$ and $r=O(k/\epsilon)$ and rank$(U) = k$. Up to constant factors, our algorithms are simultaneously optimal in $c, r,$ and rank$(U)$.

Provable Deterministic Leverage Score Sampling

We explain theoretically a curious empirical phenomenon: "Approximating a matrix by deterministically selecting a subset of its columns with the corresponding largest leverage scores results in a good low-rank matrix surrogate". To obtain provable guarantees, previous work requires randomized sampling of the columns with probabilities proportional to their leverage scores. In this work, we provide a novel theoretical analysis of deterministic leverage score sampling. We show that such deterministic sampling can be provably as accurate as its randomized counterparts, if the leverage scores follow a moderately steep power-law decay. We support this power-law assumption by providing empirical evidence that such decay laws are abundant in real-world data sets. We then demonstrate empirically the performance of deterministic leverage score sampling, which many times matches or outperforms the state-of-the-art techniques.

Random Projections for Linear Support Vector Machines

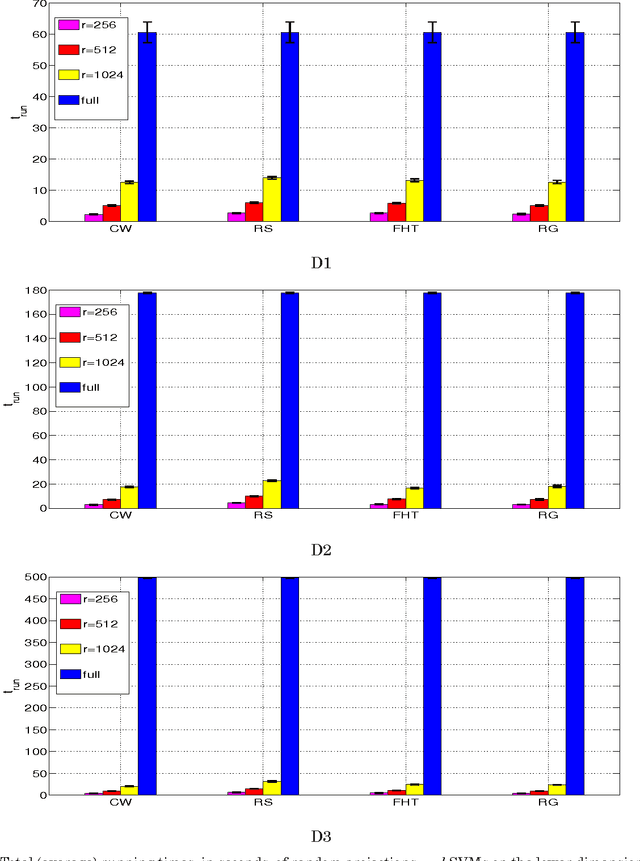
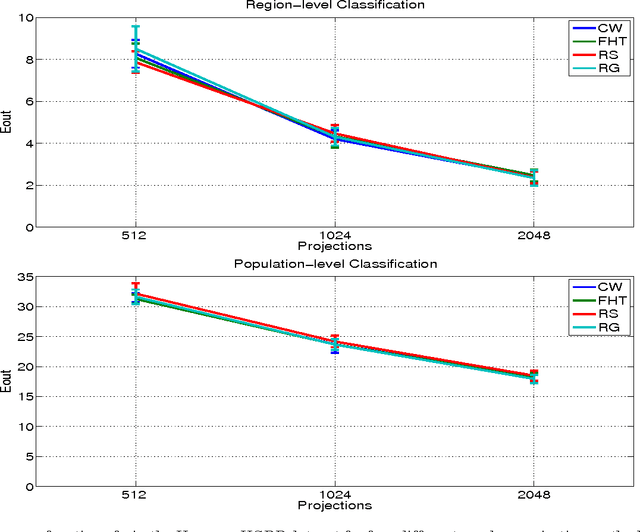
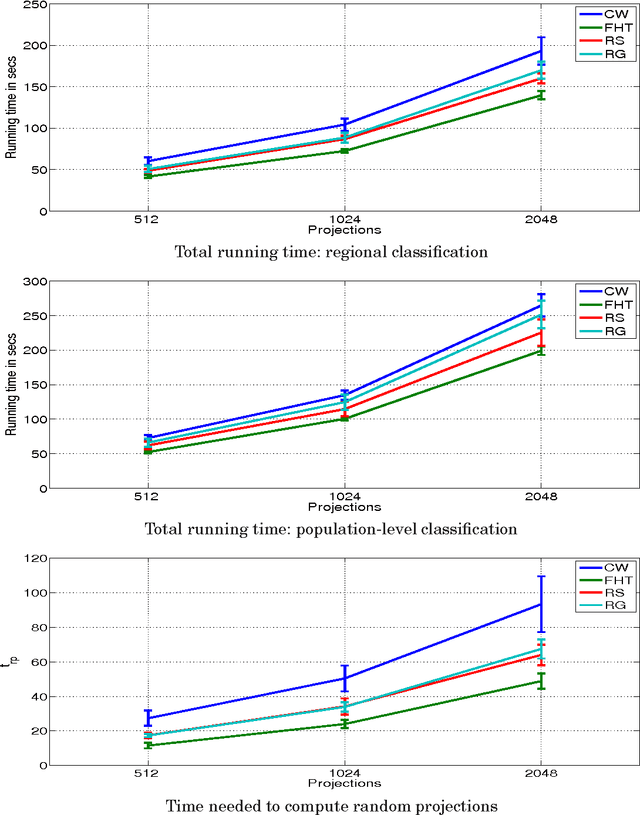
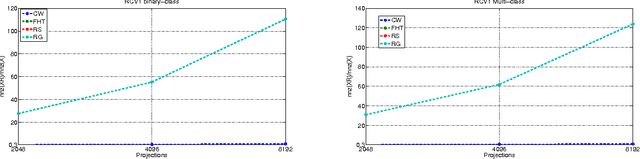
Let X be a data matrix of rank \rho, whose rows represent n points in d-dimensional space. The linear support vector machine constructs a hyperplane separator that maximizes the 1-norm soft margin. We develop a new oblivious dimension reduction technique which is precomputed and can be applied to any input matrix X. We prove that, with high probability, the margin and minimum enclosing ball in the feature space are preserved to within \epsilon-relative error, ensuring comparable generalization as in the original space in the case of classification. For regression, we show that the margin is preserved to \epsilon-relative error with high probability. We present extensive experiments with real and synthetic data to support our theory.

Near-optimal Coresets For Least-Squares Regression

We study (constrained) least-squares regression as well as multiple response least-squares regression and ask the question of whether a subset of the data, a coreset, suffices to compute a good approximate solution to the regression. We give deterministic, low order polynomial-time algorithms to construct such coresets with approximation guarantees, together with lower bounds indicating that there is not much room for improvement upon our results.

Deterministic Feature Selection for $k$-means Clustering

We study feature selection for $k$-means clustering. Although the literature contains many methods with good empirical performance, algorithms with provable theoretical behavior have only recently been developed. Unfortunately, these algorithms are randomized and fail with, say, a constant probability. We address this issue by presenting a deterministic feature selection algorithm for k-means with theoretical guarantees. At the heart of our algorithm lies a deterministic method for decompositions of the identity.

Random Projections for $k$-means Clustering

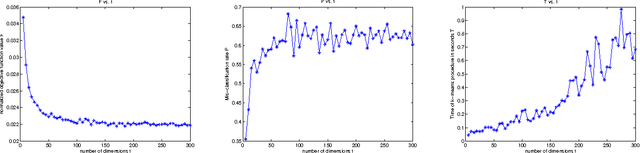
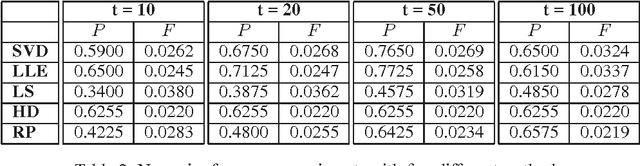
This paper discusses the topic of dimensionality reduction for $k$-means clustering. We prove that any set of $n$ points in $d$ dimensions (rows in a matrix $A \in \RR^{n \times d}$) can be projected into $t = \Omega(k / \eps^2)$ dimensions, for any $\eps \in (0,1/3)$, in $O(n d \lceil \eps^{-2} k/ \log(d) \rceil )$ time, such that with constant probability the optimal $k$-partition of the point set is preserved within a factor of $2+\eps$. The projection is done by post-multiplying $A$ with a $d \times t$ random matrix $R$ having entries $+1/\sqrt{t}$ or $-1/\sqrt{t}$ with equal probability. A numerical implementation of our technique and experiments on a large face images dataset verify the speed and the accuracy of our theoretical results.