Approaching I/O-optimality for Approximate Attention

We revisit the I/O complexity of attention in large language models. Given query-key-value matrices $Q,K,V\in\mathbb{R}^{n\times d}$, and a machine with fast memory size $M$, the goal is to compute the "attention matrix" $A=\text{softmax}(Q K ^{\top}/\sqrt{d}) V$ with the minimal number of data transfers between fast and slow memory. Existing methods in the literature, most notably FlashAttention and its variants, incur an I/O cost that depends quadratically on $n$, while a trivial lower bound only requires $Ω(nd)$ I/O's to read the inputs and write the output. In this work, we present a technique for computing attention where the I/O cost only depends almost-linearly on $n$ in most parameter regimes. This is achieved by developing I/O-efficient algorithms inspired by the recent approximate attention framework of Alman and Song. We also prove corresponding lower bounds in each parameter regime to show that our algorithms are indeed close to I/O-optimal.

Fast and Stable Triangular Inversion for Delta-Rule Linear Transformers

Linear attention has emerged as a cornerstone for efficient long-context architectures, as evidenced by its integration into state-of-the-art open-source models including Qwen3.5/3.6, Kimi Linear, and RWKV-7. Models that incorporate linear attention layers with the so-called Delta-Rule involve the inversion of triangular matrices as a core sub-routine. This operation often forms a performance bottleneck, and, due to its high-sensitivity to numerical errors, it can significantly deteriorate end-to-end model accuracy if it is not carefully implemented. This work provides a systematic analysis of both direct and iterative triangular inversion algorithms, targeting methods that are rich in matrix products, and, therefore, have the potential to efficiently utilize modern hardware. To that end, our analysis covers a broad spectrum of mathematical and practical aspects, with a heavy focus on numerical stability, computational complexity, and, ultimately, hardware efficiency and practical considerations. We provide a rigorous experimental evaluation to verify these properties in practical scenarios, and in low-precision floating-point representations, highlighting the strengths and limitations of each method. Performance benchmarks on NPUs reveal up to $4.3\times$ speed-up against the state-of-the-art implementations of SGLang for triangular matrix inversion, leading to significant performance improvements on the entire layer level, while maintaining full end-to-end model accuracy.

Branch Prediction as a Reinforcement Learning Problem: Why, How and Case Studies

Recent years have seen stagnating improvements to branch predictor (BP) efficacy and a dearth of fresh ideas in branch predictor design, calling for fresh thinking in this area. This paper argues that looking at BP from the viewpoint of Reinforcement Learning (RL) facilitates systematic reasoning about, and exploration of, BP designs. We describe how to apply the RL formulation to branch predictors, show that existing predictors can be succinctly expressed in this formulation, and study two RL-based variants of conventional BPs.

Team voyTECH: User Activity Modeling with Boosting Trees

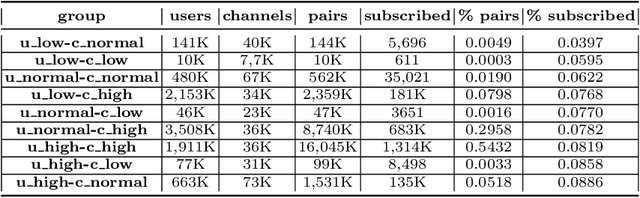
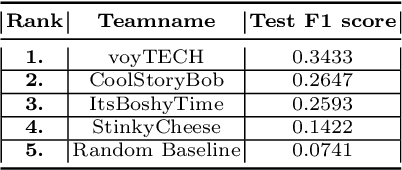
This paper describes our winning solution for the ECML-PKDD ChAT Discovery Challenge 2020. We show that whether or not a Twitch user has subscribed to a channel can be well predicted by modeling user activity with boosting trees. We introduce the connection between target-encodings and boosting trees in the context of high cardinality categoricals and find that modeling user activity is more powerful then direct modeling of content when encoded properly and combined with a suitable optimization approach.

Randomized Dimensionality Reduction for k-means Clustering

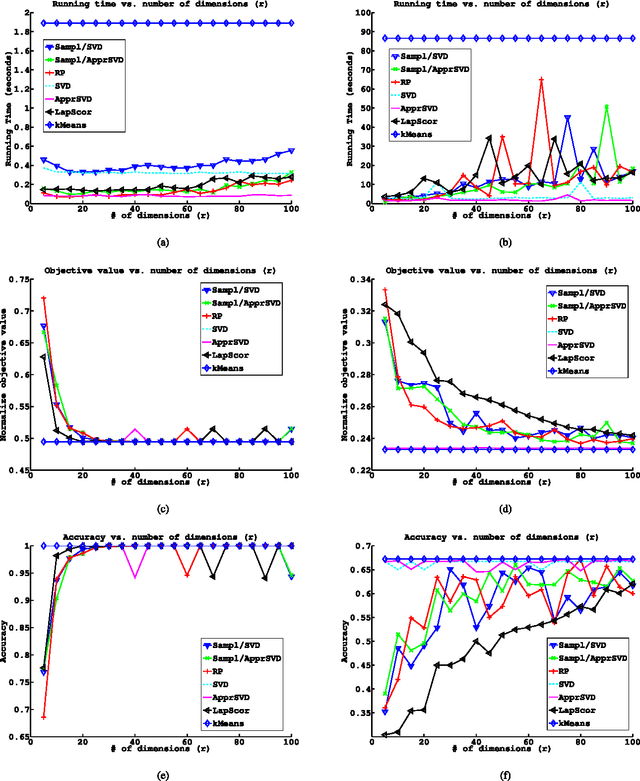
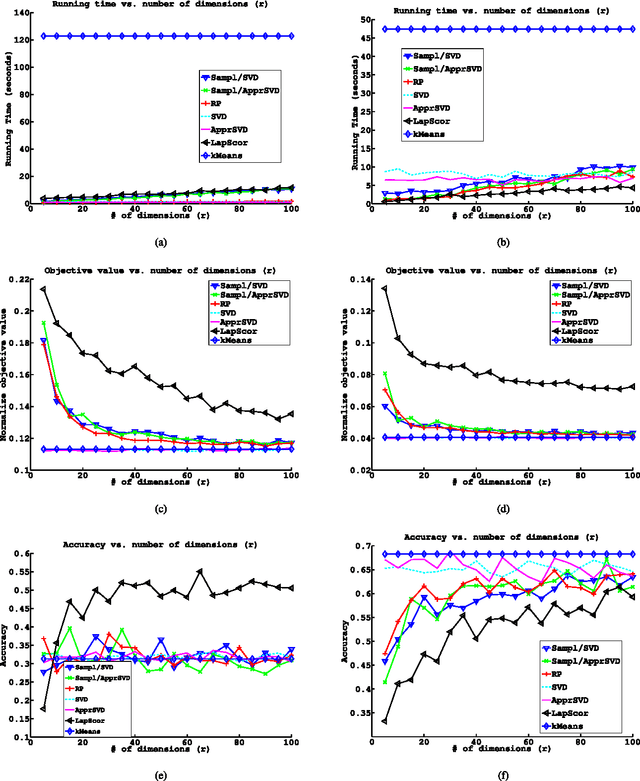
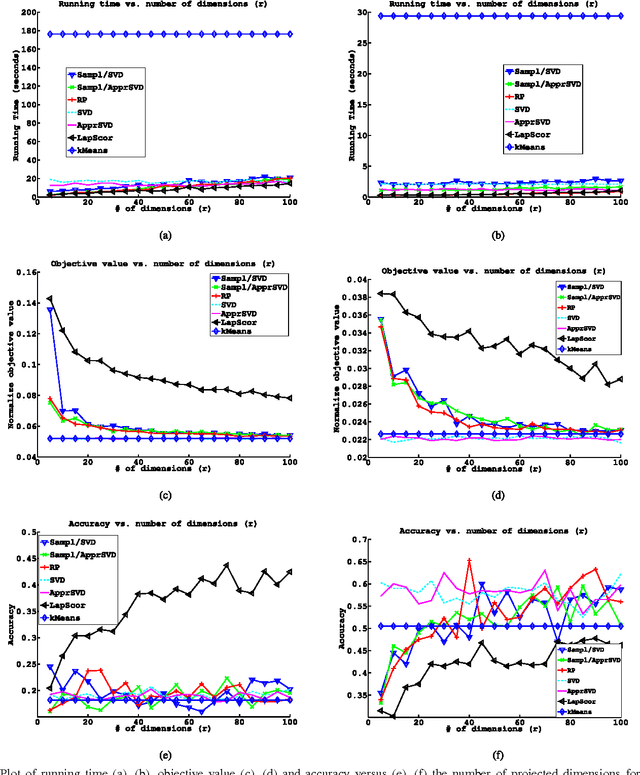
We study the topic of dimensionality reduction for $k$-means clustering. Dimensionality reduction encompasses the union of two approaches: \emph{feature selection} and \emph{feature extraction}. A feature selection based algorithm for $k$-means clustering selects a small subset of the input features and then applies $k$-means clustering on the selected features. A feature extraction based algorithm for $k$-means clustering constructs a small set of new artificial features and then applies $k$-means clustering on the constructed features. Despite the significance of $k$-means clustering as well as the wealth of heuristic methods addressing it, provably accurate feature selection methods for $k$-means clustering are not known. On the other hand, two provably accurate feature extraction methods for $k$-means clustering are known in the literature; one is based on random projections and the other is based on the singular value decomposition (SVD). This paper makes further progress towards a better understanding of dimensionality reduction for $k$-means clustering. Namely, we present the first provably accurate feature selection method for $k$-means clustering and, in addition, we present two feature extraction methods. The first feature extraction method is based on random projections and it improves upon the existing results in terms of time complexity and number of features needed to be extracted. The second feature extraction method is based on fast approximate SVD factorizations and it also improves upon the existing results in terms of time complexity. The proposed algorithms are randomized and provide constant-factor approximation guarantees with respect to the optimal $k$-means objective value.

Approximate Matrix Multiplication with Application to Linear Embeddings

In this paper, we study the problem of approximately computing the product of two real matrices. In particular, we analyze a dimensionality-reduction-based approximation algorithm due to Sarlos [1], introducing the notion of nuclear rank as the ratio of the nuclear norm over the spectral norm. The presented bound has improved dependence with respect to the approximation error (as compared to previous approaches), whereas the subspace -- on which we project the input matrices -- has dimensions proportional to the maximum of their nuclear rank and it is independent of the input dimensions. In addition, we provide an application of this result to linear low-dimensional embeddings. Namely, we show that any Euclidean point-set with bounded nuclear rank is amenable to projection onto number of dimensions that is independent of the input dimensionality, while achieving additive error guarantees.

Non-uniform Feature Sampling for Decision Tree Ensembles

We study the effectiveness of non-uniform randomized feature selection in decision tree classification. We experimentally evaluate two feature selection methodologies, based on information extracted from the provided dataset: $(i)$ \emph{leverage scores-based} and $(ii)$ \emph{norm-based} feature selection. Experimental evaluation of the proposed feature selection techniques indicate that such approaches might be more effective compared to naive uniform feature selection and moreover having comparable performance to the random forest algorithm [3]

Random Projections for $k$-means Clustering

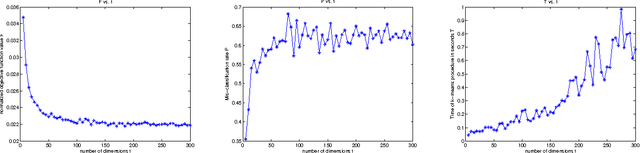
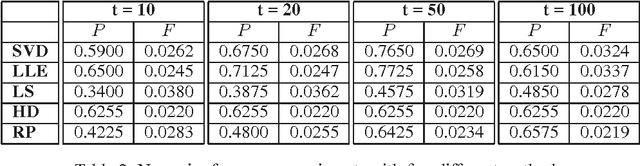
This paper discusses the topic of dimensionality reduction for $k$-means clustering. We prove that any set of $n$ points in $d$ dimensions (rows in a matrix $A \in \RR^{n \times d}$) can be projected into $t = \Omega(k / \eps^2)$ dimensions, for any $\eps \in (0,1/3)$, in $O(n d \lceil \eps^{-2} k/ \log(d) \rceil )$ time, such that with constant probability the optimal $k$-partition of the point set is preserved within a factor of $2+\eps$. The projection is done by post-multiplying $A$ with a $d \times t$ random matrix $R$ having entries $+1/\sqrt{t}$ or $-1/\sqrt{t}$ with equal probability. A numerical implementation of our technique and experiments on a large face images dataset verify the speed and the accuracy of our theoretical results.